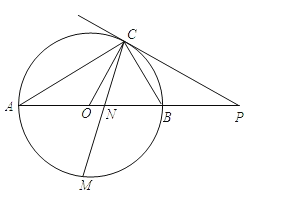
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
(1)求证:PC是⊙O的切线;
(2)点M是![]() 的中点,CM交AB于点N,若AB=6,求MNMC的值.
的中点,CM交AB于点N,若AB=6,求MNMC的值.
参考答案:
【答案】(1)详见解析;(2)18
【解析】
(1)已知C在圆上,故只需证明OC与PC垂直即可,根据圆周角定理,易得∠PCB+∠OCB=90°,即OC⊥CP,故PC是⊙O的切线;
(2)连接MA,MB,由圆周角定理可得∠ABM=∠BCM,进而可得△MBN∽△MCB,故BM2=MNMC,代入数据可得MNMC= BM2=18.
(1)证明:∵∠COB=2∠PCB,∠COB=2∠A,
∴∠A=∠PCB,
又∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠A+∠CBA=90°,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠PCB+∠OCB=90°,即OC⊥CP,
∵OC是⊙O的半径,
∴PC是⊙O的切线;
(2)连接MA、MB,
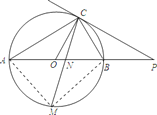
∵点M是![]() 的中点,
的中点,
∴∠ABM=∠BCM,
又∵∠BMN=∠CMB,
∴△MBN∽△MCB,
∴![]() ,即MN·MC=MB2,
,即MN·MC=MB2,
又∵AB是⊙O的直径且点M是![]() 的中点,
的中点,
∴∠AMB=90°且AM=BM,
∵AB=6,
∴BM=AM=![]() ,
,
∴MN·MC=BM2=18.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“停课不停学,学习不延期”,某市通过教育资源公共服务平台和有线电视为全市中小学开设在线“空中课堂”,为了解学生每天的学习时间情况,在全市随机抽取了部分初中学生进行问卷调查,现将调查结果绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题:
组别
学习时间x(h)
人数(人)
A
2.5<x≤3
40
B
3<x≤3.5
170
C
3.5<x≤4
350
D
4<x≤4.5
E
4.5<x≤5
90
F
5小时以上
50
表1
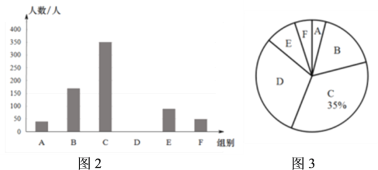
(1)这次参与问卷调查的初中学生有 人,中位数落在 组.
(2)图3中D组对应的角度是 ,并补全图2 条形统计图.
(3)若某市有初中学生2.8万人,请估计每天参与“空中课堂”学习时间3.5到4.5小时(不包括3.5小时)的初中学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,某新建火车站站前广场需要绿化的面积为35000
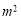 ,施工队在绿化了11000
,施工队在绿化了11000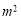 后,将每天的工作量增加为原来的1.5倍,结果提前4天完成了该项绿化工程.
后,将每天的工作量增加为原来的1.5倍,结果提前4天完成了该项绿化工程.(1)该项绿化工程原计划每天完成多少平方米?
(2)该项绿化工程中有一块长为20
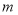 、宽为8
、宽为8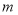 的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56
的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56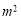 ,两块绿地之间及周边留有宽度相等的人行通道(如图②所示),则人行通道的宽度是多少米?
,两块绿地之间及周边留有宽度相等的人行通道(如图②所示),则人行通道的宽度是多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数
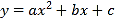 交
交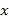 轴于点
轴于点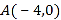 、
、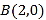 ,交
,交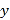 轴于点
轴于点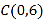 ,在
,在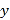 轴上有一点
轴上有一点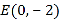 ,连接
,连接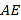 .
.
(1)求二次函数的表达式;
(2)若点
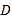 为抛物线在
为抛物线在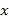 轴负半轴上方的一个动点,求
轴负半轴上方的一个动点,求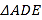 面积的最大值;
面积的最大值;(3)抛物线对称轴上是否存在点
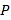 ,使
,使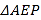 为等腰三角形,若存在,请直接写出所有
为等腰三角形,若存在,请直接写出所有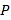 点的坐标,若不存在请说明理由.
点的坐标,若不存在请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角三角形ABC中,∠C=90°,AC=BC,E是AB的中点,过点E作AC和BC的垂线,垂足分别为点D和点F,四边形CDEF沿着CA方向匀速运动,点C与点A重合时停止运动,设运动时间为t,运动过程中四边形CDEF与△ABC的重叠部分面积为S.则S关于t的函数图象大致为( )
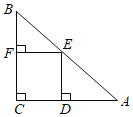
A.
 B.
B.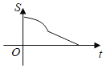 C.
C.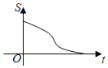 D.
D.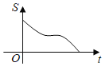
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点 A 的坐标是(﹣2,0),点 B 的坐标是(0,6),C 为 OB 的中点,将△ABC 绕点 B 逆时针旋转 90°后得到△A′B′C′.若反比例函数 y
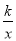 的图象恰好经过 A′B 的中点 D,则k _________.
的图象恰好经过 A′B 的中点 D,则k _________.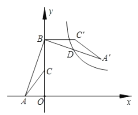
相关试题

