【题目】如图,在直角三角形ABC中,∠C=90°,AC=BC,E是AB的中点,过点E作AC和BC的垂线,垂足分别为点D和点F,四边形CDEF沿着CA方向匀速运动,点C与点A重合时停止运动,设运动时间为t,运动过程中四边形CDEF与△ABC的重叠部分面积为S.则S关于t的函数图象大致为( )
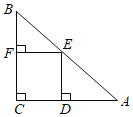
A. B.
B.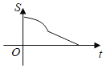 C.
C.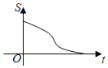 D.
D.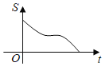
参考答案:
【答案】C
【解析】
根据已知条件得到![]() 是等腰直角三角形,推出四边形
是等腰直角三角形,推出四边形![]() 是正方形,设正方形的边长为
是正方形,设正方形的边长为![]() ,当移动的距离
,当移动的距离![]() 时,如图1,
时,如图1,![]() 正方形的面积
正方形的面积![]() △
△![]() 的面积;当移动的距离
的面积;当移动的距离![]() 时,如图2,
时,如图2,![]() ,根据函数关系式即可得到结论;
,根据函数关系式即可得到结论;
解:![]() 在直角三角形
在直角三角形![]() 中,
中,![]() ,
,![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() 是
是![]() 的中点,
的中点,
![]() ,
,![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是正方形,
是正方形,
设正方形的边长为![]() ,
,
如图1当移动的距离![]() 时,
时,![]() 正方形的面积
正方形的面积![]() △
△![]() 的面积
的面积![]() ;
;

当移动的距离![]() 时,如图2,
时,如图2,![]() ,
,
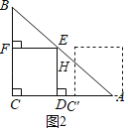
![]() 关于
关于![]() 的函数图象大致为
的函数图象大致为![]() 选项,
选项,
故选![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,某新建火车站站前广场需要绿化的面积为35000
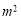 ,施工队在绿化了11000
,施工队在绿化了11000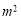 后,将每天的工作量增加为原来的1.5倍,结果提前4天完成了该项绿化工程.
后,将每天的工作量增加为原来的1.5倍,结果提前4天完成了该项绿化工程.(1)该项绿化工程原计划每天完成多少平方米?
(2)该项绿化工程中有一块长为20
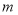 、宽为8
、宽为8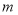 的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56
的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56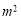 ,两块绿地之间及周边留有宽度相等的人行通道(如图②所示),则人行通道的宽度是多少米?
,两块绿地之间及周边留有宽度相等的人行通道(如图②所示),则人行通道的宽度是多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
(1)求证:PC是⊙O的切线;
(2)点M是
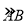 的中点,CM交AB于点N,若AB=6,求MNMC的值.
的中点,CM交AB于点N,若AB=6,求MNMC的值.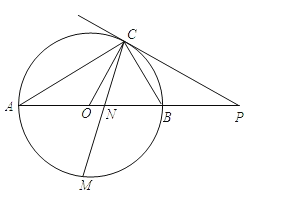
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数
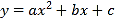 交
交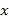 轴于点
轴于点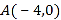 、
、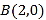 ,交
,交 轴于点
轴于点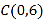 ,在
,在 轴上有一点
轴上有一点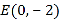 ,连接
,连接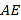 .
.
(1)求二次函数的表达式;
(2)若点
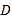 为抛物线在
为抛物线在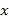 轴负半轴上方的一个动点,求
轴负半轴上方的一个动点,求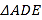 面积的最大值;
面积的最大值;(3)抛物线对称轴上是否存在点
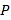 ,使
,使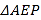 为等腰三角形,若存在,请直接写出所有
为等腰三角形,若存在,请直接写出所有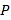 点的坐标,若不存在请说明理由.
点的坐标,若不存在请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点 A 的坐标是(﹣2,0),点 B 的坐标是(0,6),C 为 OB 的中点,将△ABC 绕点 B 逆时针旋转 90°后得到△A′B′C′.若反比例函数 y
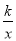 的图象恰好经过 A′B 的中点 D,则k _________.
的图象恰好经过 A′B 的中点 D,则k _________.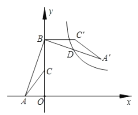
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高学生的阅读能力,我市某校开展了“读好书,助成长”的活动,并计划购置一批图书,购书前,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,请根据统计图回答下列问题:
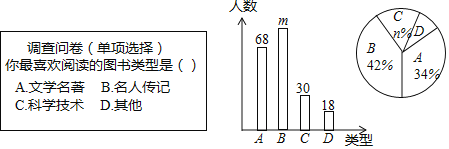
(1)本次调查共抽取了 名学生,两幅统计图中的m= ,n= .
(2)已知该校共有3600名学生,请你估计该校喜欢阅读“A”类图书的学生约有多少人?
(3)学校将举办读书知识竞赛,九年级1班要在本班3名优胜者(2男1女)中随机选送2人参赛,请用列表或画树状图的方法求被选送的两名参赛者为一男一女的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了节能减排,我市某校准备购买某种品牌的节能灯,已知3只A型节能灯和5只B型节能灯共需50元,2只A型节能灯和3只B型节能灯共需31元.
(1)求1只A型节能灯和1只B型节能灯的售价各是多少元?
(2)学校准备购买这两种型号的节能灯共200只,要求A型节能灯的数量不超过B型节能灯的数量的3倍,请设计出最省钱的购买方案,并说明理由.
相关试题

