【题目】探究归纳题:
![]()
(1)试验
如图1,直线上有两点A与B,图中有线段___条;
(2)拓展延伸:
图2直线上有A,B,C三个点,以A为端点,有线段AB,线段AC;同样以C为端点,有线段CA,线段CB;以B为端点,有线段BA,线段BC,去除重复线段,图2共有___条线段;
同样方法探究出图3中有_____条线段;
(3)探索归纳:
如果直线上有n(n为正整数)个点,则共有________条线段.(用含n的式子表示)
(4)解决问题:
①中职篮(CBA)2018——2019赛季,比赛队伍数仍然为20支,截止2018年12月14日,赛程已经过半(每两队之间都赛了一场),请你帮助计算一下目前一共进行了多少场比赛?
②2018年11月30日,赤峰至京沈高铁喀左站客运专线路基工程全部完成,将正式进入轨道铺设阶段,预计2020年7月1日通车,北京至赤峰有北京星火站,顺义西站,怀柔南站,密云站,兴隆西站,安匠站,承德南站,承德县北站,平泉北站,牛河梁站,喀左站,宁城站、平庄西站、赤峰西站等共计14个车站,请你帮助计算一下,应该设计多少种高铁车票?
参考答案:
【答案】(1)1条;(2)3条;6条;(3)![]() ;(4)①190场;②182种.
;(4)①190场;②182种.
【解析】
(1)根据两点确定一条线段即可解题,
(2)根据线段的定义,对字母进行排列即可解题,
(3)每一个点都能作出(n-1)个线段,n个点一共有n(n-1)个线段,除去重复的即可解题,
(4)①根据上一问公式求出总场数,除以2即可解题, ②根据上一问公式求出所有可能性,因为路线有方向性,所以不用除以2.
(1)1条
(2)3条,6条
(3)每一个点都能作出(n-1)个线段,n个点一共有n(n-1)个线段,除去重复的所以共有![]() 条线段.
条线段.
(4)①20×(20-1)÷2=190场
②14×(14-1)=182种
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)叙述并证明三角形内角和定理(证明用图 1);
(2)如图 2 是七角星形,求∠A+∠B+∠C+∠D+∠E+∠F+∠G 的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】大润发超市在销售某种进货价为20元/件的商品时,以30元/件售出,每天能售出100件.调查表明:这种商品的售价每上涨1元/件,其销售量就将减少2件.
(1)为了实现每天1600元的销售利润,超市应将这种商品的售价定为多少?
(2)设每件商品的售价为x元,超市所获利润为y元. ①求y与x之间的函数关系式;
②物价局规定该商品的售价不能超过40元/件,超市为了获得最大的利润,应将该商品售价定为多少?最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为等边三角形,D为边BA延长线上一点,连接CD,以CD为一边作等边三角形CDE,连接AE.
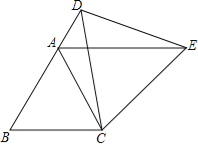
(1)求证:△CBD≌△CAE.
(2)判断AE与BC的位置关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场对一种新售的手机进行市场问卷调查,其中一个项目是让每个人按A(不喜欢)、B(一般)、C(不比较喜欢)、D(非常喜欢)四个等级对该手机进行评价,图①和图②是该商场采集数据后,绘制的两幅不完整的统计图,请你根据以上统计图提供的信息,回答下列问题:
(1)本次调查的人数为多少人?A等级的人数是多少?请在图中补全条形统计图.
(2)图①中,a等于多少?D等级所占的圆心角为多少度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C为⊙O上一点,AD⊥CD,(点D在⊙O外)AC平分∠BAD.
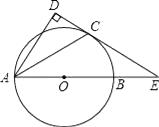
(1)求证:CD是⊙O的切线;
(2)若DC、AB的延长线相交于点E,且DE=12,AD=9,求BE的长. -
科目: 来源: 题型:
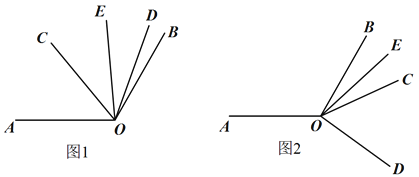
查看答案和解析>>【题目】已知∠AOB=120°,∠COD=60°,OE平分∠BOC
(1)如图1.当∠COD在∠AOB的内部时
①若∠AOC=39°40′,求∠DOE的度数;
②若∠AOC=α,求∠DOE的度数(用含α的代数式表示),
(2)如图2,当∠COD在∠AOB的外部时,(1)中∠AOC与∠DOE的数量关系还成立吗?若成立,请推导出∠AOC与∠DOE的度数之间的关系;若不成立,请说明理由.
相关试题

