【题目】已知∠AOB=120°,∠COD=60°,OE平分∠BOC
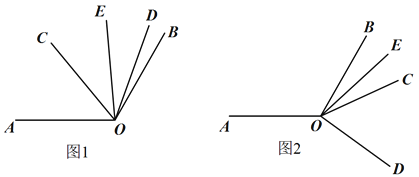
(1)如图1.当∠COD在∠AOB的内部时
①若∠AOC=39°40′,求∠DOE的度数;
②若∠AOC=α,求∠DOE的度数(用含α的代数式表示),
(2)如图2,当∠COD在∠AOB的外部时,(1)中∠AOC与∠DOE的数量关系还成立吗?若成立,请推导出∠AOC与∠DOE的度数之间的关系;若不成立,请说明理由.
参考答案:
【答案】(1)①19°50′;②![]() α;(2)∠AOC=2∠DOE的关系成立;理由见解析.
α;(2)∠AOC=2∠DOE的关系成立;理由见解析.
【解析】
(1)①由∠AOB=120°,∠COD=60°得∠BOC=80°20′,根据角平分线得∠DOE=19°50′;
②方法同上,见详解,
(2)根据题意得∠AOC=120°+∠BOC,利用角平分线得∠DOE=60°+![]() ∠BOC,即可解题.
∠BOC,即可解题.
解:(1)①∵∠AOB=120°,∠COD=60°,∠AOC=39°40′,
∴∠BOC=∠AOB﹣∠AOC=120°﹣39°40′=80°20′,
∵OE平分∠BOC,
∴∠COE=![]() ∠BOC=40°10′,
∠BOC=40°10′,
∴∠DOE=∠COD﹣∠COE=19°50′;
②∵∠AOB=120°,∠COD=60°,∠AOC=α,
∴∠BOC=∠AOB﹣∠AOC=120°﹣α,
∵OE平分∠BOC,
∴∠COE=![]() ∠BOC=60°﹣
∠BOC=60°﹣![]() α,
α,
∴∠DOE=![]() α;
α;
(2)(1)中∠AOC=2∠DOE的关系成立;
理由是:∵∠AOC=120°+∠BOC,∠DOE=60°+∠COE,
∵OE平分∠BOC,
∴∠COE=![]() ∠BOC,
∠BOC,
∴∠DOE=60°+![]() ∠BOC
∠BOC
∴2∠DOE=120°+∠BOC
∴∠AOC=2∠DOE;
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究归纳题:
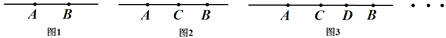
(1)试验
如图1,直线上有两点A与B,图中有线段___条;
(2)拓展延伸:
图2直线上有A,B,C三个点,以A为端点,有线段AB,线段AC;同样以C为端点,有线段CA,线段CB;以B为端点,有线段BA,线段BC,去除重复线段,图2共有___条线段;
同样方法探究出图3中有_____条线段;
(3)探索归纳:
如果直线上有n(n为正整数)个点,则共有________条线段.(用含n的式子表示)
(4)解决问题:
①中职篮(CBA)2018——2019赛季,比赛队伍数仍然为20支,截止2018年12月14日,赛程已经过半(每两队之间都赛了一场),请你帮助计算一下目前一共进行了多少场比赛?
②2018年11月30日,赤峰至京沈高铁喀左站客运专线路基工程全部完成,将正式进入轨道铺设阶段,预计2020年7月1日通车,北京至赤峰有北京星火站,顺义西站,怀柔南站,密云站,兴隆西站,安匠站,承德南站,承德县北站,平泉北站,牛河梁站,喀左站,宁城站、平庄西站、赤峰西站等共计14个车站,请你帮助计算一下,应该设计多少种高铁车票?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场对一种新售的手机进行市场问卷调查,其中一个项目是让每个人按A(不喜欢)、B(一般)、C(不比较喜欢)、D(非常喜欢)四个等级对该手机进行评价,图①和图②是该商场采集数据后,绘制的两幅不完整的统计图,请你根据以上统计图提供的信息,回答下列问题:
(1)本次调查的人数为多少人?A等级的人数是多少?请在图中补全条形统计图.
(2)图①中,a等于多少?D等级所占的圆心角为多少度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C为⊙O上一点,AD⊥CD,(点D在⊙O外)AC平分∠BAD.
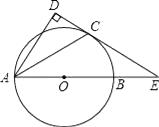
(1)求证:CD是⊙O的切线;
(2)若DC、AB的延长线相交于点E,且DE=12,AD=9,求BE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△DEC中,AB=DE.若添加条件后使得△ABC≌△DEC,则在下列条件中,不能添加的是( )

A. BC=EC,∠B=∠E B. BC=EC,AC=DC
C. ∠B=∠E,∠A=∠D D. BC=EC,∠A=∠D
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
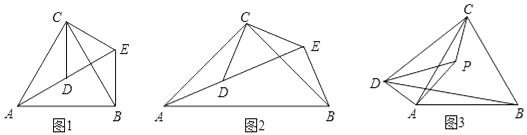
(1)问题发现:如图1,△ACB和△DCE均为等边三角形,当△DCE旋转至点A,D,E在同一直线上,连接BE,易证△BCE≌△ACD.则
①∠BEC=°;②线段AD、BE之间的数量关系是 .
(2)拓展研究:
如图2,△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=90°,点A、D、E在同一直线上,若AE=15,DE=7,求AB的长度.
(3)探究发现:
如图3,P为等边△ABC内一点,且∠APC=150°,且∠APD=30°,AP=5,CP=4,DP=8,求BD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF、CE,且∠FBD=35°,∠BDF=75°,下列说法:①△BDF≌CDE;②ABD和△ACD面积相等;③BF∥CE;④∠DEC=70°,其中正确的有( )
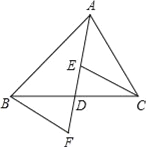
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

