【题目】已知直线y=kx+b(k≠0)过点(1,2)
(1)填空:b= (用含k代数式表示);
(2)将此直线向下平移2个单位,设平移后的直线交x于点A,交y于点B,x轴上另有点C(1+k,0),使得△ABC的面积为2,求k值;
(3)当1≤x≤3,函数值y总大于零,求k取值范围.
参考答案:
【答案】(1)2﹣k;(2)k=±2;(3)当k>0或﹣1<k<0时,函数值y总大于0.
【解析】(1)∵直线y=kx+b(k≠0)过点(1,2),
∴k+b=2,
∴b=2﹣k.
故答案为2﹣k;
(2)由(1)可得y=kx+2﹣k,
向下平移2个单位所得直线的解析式为y=kx﹣k,
令x=0,得y=﹣k,令y=0,得x=1,
∴A(1,0),B(0,﹣k),
∵C(1+k,0),
∴AC=|1+k﹣1|=|k|,
∴S△ABC=![]() AC|yB|=
AC|yB|=![]() |k||﹣k|=
|k||﹣k|=![]() k2,
k2,
∴![]() k2=2,解得k=±2;
k2=2,解得k=±2;
(3)依题意,当自变量x在1≤x≤3变化时,函数值y的最小值大于0.
分两种情况:
ⅰ)当k>0时,y随x增大而增大,
∴当x=1时,y有最小值,最小值为k+2﹣k=2>0,
∴当 k>0时,函数值总大于0;
ⅱ)当k<0时,y随x增大而减小,
∴当x=3时,y有最小值,最小值为3k+2﹣k=2k+2,
由2k+2>0得k>﹣1,
∴﹣1<k<0.
综上,当k>0或﹣1<k<0时,函数值y总大于0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(3,4)先向左平移5个单位,再向下平移2个单位得到点B,则点B的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在我国南海某海域探明可燃冰储量约有194亿立方米.194亿用科学记数法表示为( )
A.1.94×1010
B.0.194×1010
C.19.4×109
D.1.94×109 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△BCD中,∠BAC=∠BCD=90°,AB=AC,CB=CD.延长CA至点E,使AE=AC;延长CB至点F,使BF=BC.连接AD,AF,DF,EF.延长DB交EF于点N.
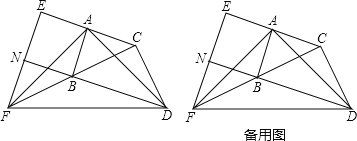
(1)求证:AD=AF;
(2)求证:BD=EF;
(3)试判断四边形ABNE的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)3
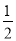 +(-
+(-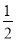 )-(-
)-(-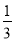 )+2
)+2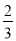 (2)(
(2)(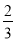 -
-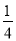 -
- +
+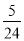 )×48
)×48(3)
 (4)
(4) 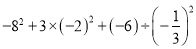
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系为: .
②BC,CD,CF之间的数量关系为: ;(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2
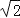 ,CD=
,CD=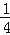 BC,请求出GE的长.
BC,请求出GE的长.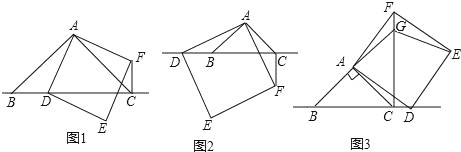
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在正方形ABCD中,点E在边BC上,点F在边CD的延长线上,且BE=DF.
(1)求∠AEF的度数;
(2)如果∠AEB=75°,AB=2,求△FEC的面积.
相关试题

