【题目】在△ABC中,AB=AC,CD是AB边上的中线,点E在边AC上(不与A,C重合),且BE=CD.设![]() =k,若符合条件的点E有两个,则k的取值范围是_____.
=k,若符合条件的点E有两个,则k的取值范围是_____.
参考答案:
【答案】![]() 且
且![]()
【解析】
符合条件的点E有两个E、E1,则AC边上的高垂直平分EE1,由等腰三角形的性质得出BE是中线,AE=CE,求出当CD⊥AB时,BE⊥AC,满足条件的点E有一个,此时△ABC是等边三角形,AB=BC,![]() =1;求出当满足条件的一个点E1与点A重合时,
=1;求出当满足条件的一个点E1与点A重合时,![]() =
=![]() ;当满足条件的一个点E1与点C重合时,BE=BC,证明△BCE∽△ABC,得出
;当满足条件的一个点E1与点C重合时,BE=BC,证明△BCE∽△ABC,得出![]() =
=![]() ,求出AB=
,求出AB=![]() BC,得出
BC,得出![]() =
=![]() ,即可得出结果.
,即可得出结果.
解:设![]() =k,若符合条件的点E有两个E、E1,
=k,若符合条件的点E有两个E、E1,
则AC边上的高垂直平分EE1,
∵AB=AC,CD是AB边上的中线,BE=CD,
∴BE是中线,AE=CE,
当CD⊥AB时,BE⊥AC,满足条件的点E有一个,
此时△ABC是等边三角形,AB=BC,
![]() =1;
=1;
当满足条件的一个点E1与点A重合时,BE=AB,
作BG⊥AC于G,如下图所示:
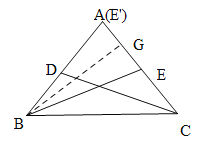
则AG=EG=![]() AE=
AE=![]() AC=
AC=![]() AB,
AB,
由勾股定理得:BG2=AB2-AG2,
BC2=BG2+CG2=AB2-AG2+CG2=AB2-(![]() AB)2+(
AB)2+(![]() AB)2=
AB)2=![]() AB2,
AB2,
∴BC=![]() AB,
AB,
∴![]() =
=![]() ;
;
当满足条件的一个点E1与点C重合时,BE=BC,
如下图所示:
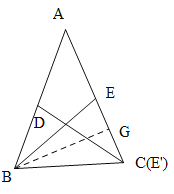
∴∠BCE=∠BEC,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠BCE=∠BEC=∠ABC=∠ACB,
∴△BCE∽△ABC,
∴![]() =
=![]() ,
,
∴BC2=AB×CE=![]() AB2,
AB2,
∴AB=![]() BC,
BC,
∴![]() =
=![]() ;
;
综上所述,设![]() =k,若符合条件的点E有两个,则k的取值范围是:
=k,若符合条件的点E有两个,则k的取值范围是:![]() <k<
<k<![]() ,且k≠1;
,且k≠1;
故答案为![]() <k<
<k<![]() ,且k≠1.
,且k≠1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD的四个角向内折起,恰好拼成一个无缝隙,无重叠的四边形EFGH,设AB=a,BC=b,若AH=1,则( )
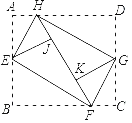
A.a2=4b﹣4B.a2=4b+4C.a=2b﹣1D.a=2b+1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左侧墙上与地面成60°角时,梯子顶端距离地面2
 米,若保持梯子底端位置不动,将梯子斜靠在右端时,与地面成45°,则小巷的宽度为_____米(结果保留根号).
米,若保持梯子底端位置不动,将梯子斜靠在右端时,与地面成45°,则小巷的宽度为_____米(结果保留根号).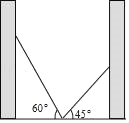
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
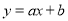 ,反比例函数
,反比例函数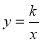 (a,b,k是常数,且
(a,b,k是常数,且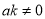 ),若其中一部分x,y的对应值如表:则不等式
),若其中一部分x,y的对应值如表:则不等式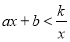 的解集是_________.
的解集是_________.x

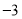
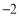
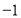
1
2
3
4
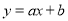
3
2
1
0
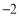
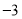

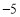
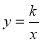
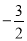
2
3
6
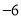
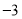
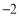
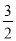
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解八年级学生的户外活动情况,某校随机调查了该年级部分学生双休日户外活动的时间(单位:小时),调查结果按0~1,1~2,2~3,3~4(每组含前一个边界值,不含后一个边界值)分为四个等级,并依次用A,B,C,D表示,调查人员整理数据并绘制了如图所示的不完整的统计图,请根据所给信息解答下列问题.
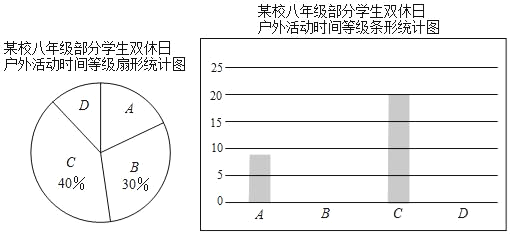
(1)求本次调查的学生人数.
(2)求等级D的学生人数,并补全条形统计图.
(3)该年级共有600名学生,估计该年级学生双休日户外活动时间不少于2小时的人数.
-
科目: 来源: 题型:
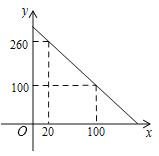
查看答案和解析>>【题目】为了清洗水箱,需先放掉水箱内原有的存水,如图是水箱剩余水量y(升)随放水时间x(分)变化的图象.
(1)求y关于x的函数表达式,并确定自变量x的取值范围;
(2)若8:00打开放水龙头,估计8:55﹣9:10(包括8:55和9:10)水箱内的剩水量(即y的取值范围);
(3)当水箱中存水少于10升时,放水时间至少超过多少分钟?
-
科目: 来源: 题型:
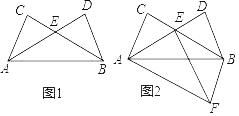
查看答案和解析>>【题目】如图1,点C、D是线段AB同侧两点,且AC=BD,∠CAB=∠DBA,连接BC,AD交于点 E.
(1)求证:AE=BE;
(2)如图2,△ABF与△ABD关于直线AB对称,连接EF.
①判断四边形ACBF的形状,并说明理由;
②若∠DAB=30°,AE=5,DE=3,求线段EF的长.
相关试题

