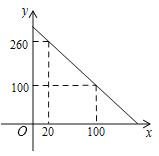
【题目】为了清洗水箱,需先放掉水箱内原有的存水,如图是水箱剩余水量y(升)随放水时间x(分)变化的图象.
(1)求y关于x的函数表达式,并确定自变量x的取值范围;
(2)若8:00打开放水龙头,估计8:55﹣9:10(包括8:55和9:10)水箱内的剩水量(即y的取值范围);
(3)当水箱中存水少于10升时,放水时间至少超过多少分钟?
参考答案:
【答案】(1)y=-2x+300(0≤x≤150);(2)160≤y≤190;(3)至少超过145min;
【解析】
(1)根据函数图象中的数据可以求得y关于x的函数表达式,并写出自变量x的取值范围;
(2)根据题意和(1)中的函数关系式可以求得y的取值范围;
(3)根据题意可以得关于x的不等式,从而可以解答本题.
![]() 设函数表达式为
设函数表达式为![]()
把![]() 时,
时,![]() ;把
;把![]() 时,
时,![]() 代入,得
代入,得
![]()
解得![]()
![]()
由![]() ,得
,得![]()
∴自变量![]() 的取值范围是
的取值范围是![]()
(2)∵当![]() 时,
时,![]()
当![]() 时,
时,![]()
∴水箱内的剩余水量160≤y≤190
(3)由![]() ,得
,得![]()
即当水箱中存水少于10升时,放水时间至少超过145分钟
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
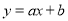 ,反比例函数
,反比例函数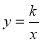 (a,b,k是常数,且
(a,b,k是常数,且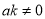 ),若其中一部分x,y的对应值如表:则不等式
),若其中一部分x,y的对应值如表:则不等式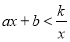 的解集是_________.
的解集是_________.x

1
2
3
4
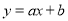
3
2
1
0
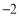
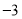

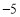
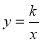
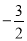
2
3
6
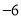
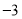
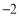
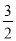
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,CD是AB边上的中线,点E在边AC上(不与A,C重合),且BE=CD.设
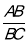 =k,若符合条件的点E有两个,则k的取值范围是_____.
=k,若符合条件的点E有两个,则k的取值范围是_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解八年级学生的户外活动情况,某校随机调查了该年级部分学生双休日户外活动的时间(单位:小时),调查结果按0~1,1~2,2~3,3~4(每组含前一个边界值,不含后一个边界值)分为四个等级,并依次用A,B,C,D表示,调查人员整理数据并绘制了如图所示的不完整的统计图,请根据所给信息解答下列问题.
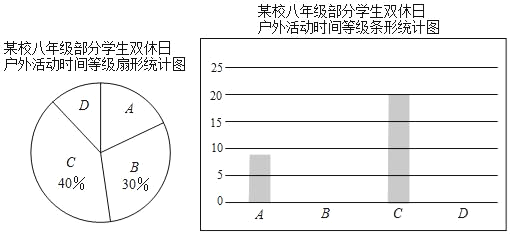
(1)求本次调查的学生人数.
(2)求等级D的学生人数,并补全条形统计图.
(3)该年级共有600名学生,估计该年级学生双休日户外活动时间不少于2小时的人数.
-
科目: 来源: 题型:
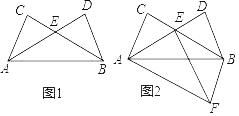
查看答案和解析>>【题目】如图1,点C、D是线段AB同侧两点,且AC=BD,∠CAB=∠DBA,连接BC,AD交于点 E.
(1)求证:AE=BE;
(2)如图2,△ABF与△ABD关于直线AB对称,连接EF.
①判断四边形ACBF的形状,并说明理由;
②若∠DAB=30°,AE=5,DE=3,求线段EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设二次函数y1=ax2+bx+a﹣5(a,b为常数,a≠0),且2a+b=3.
(1)若该二次函数的图象过点(﹣1,4),求该二次函数的表达式;
(2)y1的图象始终经过一个定点,若一次函数y2=kx+b(k为常数,k≠0)的图象也经过这个定点,探究实数k,a满足的关系式;
(3)已知点P(x0,m)和Q(1,n)都在函数y1的图象上,若x0<1,且m>n,求x0的取值范围(用含a的代数式表示).
-
科目: 来源: 题型:
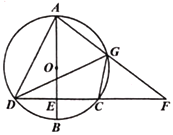
查看答案和解析>>【题目】如图,
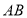 是
是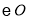 的直径,弦
的直径,弦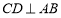 于点
于点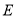 ,
,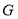 是
是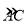 上一点,
上一点,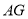 ,
,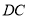 的延长线交于点
的延长线交于点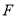 ,连接
,连接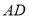 ,
,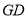 ,
,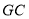 .
.
(1)求证:
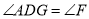 .
.(2)已知
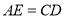 ,
,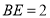 .
.①求
 的半径长.
的半径长.②若点
 是
是 的中点,求
的中点,求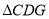 与
与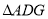 的面积之比.
的面积之比.
相关试题

