【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足若 ![]() =
= ![]() ,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.
,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3. 
(1)求证:△ADF∽△AED;
(2)求FG的长;
(3)求tan∠E的值.
参考答案:
【答案】
(1)证明:∵AB是⊙O的直径,弦CD⊥AB,
∴DG=CG,
∴由垂径定理可知: ![]() ,
,
∴∠ADF=∠AED,
∵∠FAD=∠DAE(公共角),
∴△ADF∽△AED
(2)解:∵ ![]() =
= ![]() ,CF=2,
,CF=2,
∴FD=6,
∴CD=DF+CF=8,
∴由垂径定理可知:CG=DG=4,
∴FG=CG﹣CF=2
(3)解:∵AF=3,FG=2,
在△AFG中,
∴由勾股定理可知:AG= ![]() =
= ![]() ,
,
tan∠E=tan∠ADF= ![]() =
= ![]()
【解析】(1)AB是⊙O的直径,弦CD⊥AB,DG=CG,由垂径定理可知: ![]() ,从而可知∠ADF=∠AED,从而可证明△ADF∽△AED.(2)由于
,从而可知∠ADF=∠AED,从而可证明△ADF∽△AED.(2)由于 ![]() =
= ![]() ,所以CF=2,FD=6,从而CD=DF+CF=8,由垂径定理可知CD=DG=4,从而求出FG的长度;(3)由于AF=3,FG=2,由勾股定理可知:AG=
,所以CF=2,FD=6,从而CD=DF+CF=8,由垂径定理可知CD=DG=4,从而求出FG的长度;(3)由于AF=3,FG=2,由勾股定理可知:AG= ![]() =
= ![]() ,从而可知tan∠E=tan∠ADF=
,从而可知tan∠E=tan∠ADF= ![]() =
= ![]() .
.
【考点精析】关于本题考查的勾股定理的概念和垂径定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校学生会为了解本校初中学生每天做作业所用时间情况,采用问卷的方式对一部分学生进行调查.在确定调查对象时,大家提出以下几种方案:A.对各班班长进行调查;B.对某班的全体学生进行调查;C.从全校每班随机抽取5名学生进行调查.在问卷调查时,每位被调查的学生都选择了问卷中适合自己的一个时间,学生会将收集到的数据整理后绘制成如图所示的条形统计图.
(1)为了使收集到的数据具有代表性.学生会在确定调查对象时应选择方案________ (填A,B或C);
(2)被调查的学生每天做作业所用时间的众数为________h;
(3)根据以上统计结果,估计该校900名初中学生中每天做作业用1.5 h的人数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
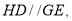 点
点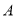 在直线
在直线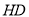 上,点
上,点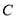 在直线
在直线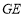 上,点
上,点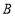 在直线
在直线 之间,
之间,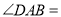
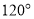 .
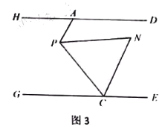
.(1)如图1,若
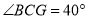 ,求
,求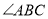 的度数;
的度数;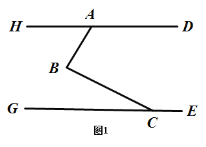
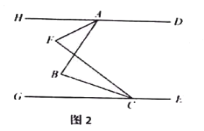
(2)如图2,
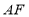 平分
平分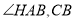 平分
平分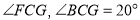 ,比较
,比较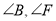 的大小;
的大小;(3)如图3,点
 是线段
是线段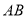 上一点,
上一点,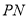 平分
平分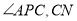 平分
平分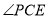 ,探究
,探究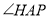 和
和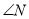 的数量关系,并说明理由.
的数量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了抓住梵净山文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】某服装店用4400元购进A,B两种新式服装,按标价售出后可获得毛利润2800元(毛利润=售价﹣进价),这两种服装的进价,标价如表所示.
类型价格
A型
B型
进价(元/件)
60
100
标价(元/件)
100
160
(1)请利用二元一次方程组求这两种服装各购进的件数;
(2)如果A种服装按标价的9折出售,B种服装按标价的8折出售,那么这批服装全部售完后,服装店比按标价出售少收入多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小张骑自行车匀速从甲地到乙地,在途中因故停留了一段时间后,仍按原速骑行,小李骑摩托车比小张晚出发一段时间,以800米/分的速度匀速从乙地到甲地,两人距离乙地的路程y(米)与小张出发后的时间x(分)之间的函数图象如图所示.
(1)求小张骑自行车的速度;
(2)求小张停留后再出发时y与x之间的函数表达式;
(3)求小张与小李相遇时x的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形OABC和正方形CDEF在平面直角坐标系中,点O,C,F在y轴上,点O为坐标原点,点M为OC的中点,抛物线y=ax2+b经过M,B,E三点,则
 的值为 .
的值为 . 
相关试题

