【题目】已知二次函数 ![]() 的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,顶点为D.
的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,顶点为D.
(1)求以A,B,C,D为顶点的四边形的面积;
(2)在抛物线上是否存在点P,使得△ABP的面积是△ABC的面积的2倍?若存在,求出点P的坐标;若不存在,请说明理由。
参考答案:
【答案】
(1)解:令y=0, x26x+5=0 ,
∴ x1=1,x2=5,
∴A(1,0),B(5,0),
令x=0,
∴y=5,
∴C(0,5)
∵ y=x26x+5=(x3)24 ,
∴D(3,-4)
∴S四边形ACBD=S△ABD+S△ABC=![]() +
+![]() =18 .
=18 .
(2)解:∵ S△ABP=2S△ABC,且两个三角形底边相同,
∴ |yP|=2|yC|=10 ,
又∵ ymin=4 ,
∴ yP=10 ,
∴ P1(3+![]() ,10),P2(3-
,10),P2(3-![]() ,10).
,10).
【解析】(1)根据题意令y=0得出A(1,0),B(5,0),令x=0得C(0,5),将抛物线解析式化成顶点式得 D(3,-4),从而求出
∴S四边形ACBD=S△ABD+S△ABC=![]() +
+![]() =18 .
=18 .
(2)根据 S△ABP=2S△ABC,且底边相同,得出|yP|=2|yC|=10 ,再由已知条件得yP=10 , 从而得P点坐标为 P1(3+![]() ,10),P2(3-
,10),P2(3-![]() ,10).
,10).
【考点精析】认真审题,首先需要了解抛物线与坐标轴的交点(一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.),还要掌握三角形的面积(三角形的面积=1/2×底×高)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),E是直线AB、CD内部一点,AB∥CD,连接EA、ED.
(1)探究:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③在图(1)中∠AED、∠EAB、∠EDC有什么数量关系,并证明你的结论.
(2)拓展:如图(2),射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的四个区域(不含边界,其中③④位于直线AB的上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF之间的关系.(不要求证明)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知点D、E、F分别是BC、AD、BE上的中点,且△ABC的面积为8cm2,则△CEF的面积为( )

A.0.5cm2B.1cm2C.2cm2D.4cm2
-
科目: 来源: 题型:
查看答案和解析>>【题目】在湖州创建国家卫生文明城市的过程中,张辉和夏明积极参加志愿者活动,当时有下列四个志愿者工作岗位供他们选择:①清理类岗位:清理花坛卫生死角;清理楼道杂物(分别用
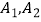 表示)。
表示)。
②宣传类岗位:垃圾分类知识宣传;交通安全知识宣传(分别用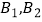 表示)。
表示)。
(1)张辉同学从四个岗位中随机选取一个报名,恰好选择清理类岗位概率为是;
(2)若张辉和夏明各随机从四个岗位中选一个报名,请你利用树状图或列表法求出他们恰好都选择同一个岗位的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB是⊙O的直径,C是圆周上的动点,P是优弧中点.

(1)求证:OP∥BC.
(2)连接PC交直径AB于点D,当OC=DC时,求∠A的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两个完全相同的直角三角形纸片△ABC、△DEF,如图1放置,点B、D重合,点F在BC上,AB与EF交于点G.∠C=∠EFB=90°,∠E=∠ABC=30°,现将图1中的△ABC绕点F按每秒10°的速度沿逆时针方向旋转180°,在旋转的过程中,△ABC恰有一边与DE平行的时间为___________s

-
科目: 来源: 题型:
查看答案和解析>>【题目】探究:22﹣21=2×21﹣1×21=2( )
23﹣22= =2( ),
24﹣23= =2( ),
……
(1)请仔细观察,写出第4个等式;
(2)请你找规律,写出第n个等式;
(3)计算:21+22+23+…+22019﹣22020.
相关试题

