搜索
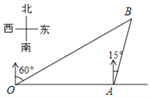
【题目】如图，港口A在观测站O的正东方向，OA=6km，某船从港口A出发，沿北偏东15°方向航行一段距离后到达B处，此时从观测站O处测得该船位于北偏东60°的方向，则该船航行的距离（即AB的长）为（ ）
A. 3
km B. 3
km C. 4km D. （3
-3）km
参考答案：
【答案】A
【解析】如图，如图，过点A作AD⊥OB于D．在Rt△AOD中，∠ADO=90°，∠AOD=30°，OA=6 km，根据在直角三角形中30°的锐角所对的直角边等于斜边的一半可得AD=3 km．在Rt△ABD中，∠ADB=90°，∠B=∠CAB-∠AOB=75°-30°=45°，根据等腰直角三角形的性质可得BD=AD=3 km，由勾股定理可得AB=3
km，即该船航行的距离（即AB的长）为3
km．故选A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】“十一”黄金周期间，淮安动物园在7天假期中每天接待的人数变化如下表(正数表示比前一天多的人数，负数表示比前一天少的人数)，把9月30日的游客人数记为a万人．
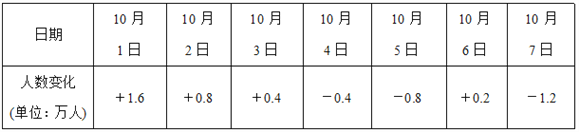
(1)请用含a的代数式表示10月2日的游客人数；
(2)请判断七天内游客人数最多的是哪天，有多少人？
(3)若9月30日的游客人数为2万人，门票每人10元，问黄金周期间淮安动物园门票收入是多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】《九章算术》卷九“勾股”中记载：今有户不知高广，竿不知长短.横之不出四尺，纵之不出二尺，斜之适出注.问户斜几何.
注释：横放，竿比门宽长出四尺；竖放，竿比门高长出二尺；斜放恰 好能出去.解决下列问题：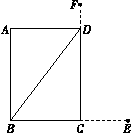
（1）示意图中，线段CE的长为尺，线段DF的长为尺；
（2）求户斜多长. -
科目： 来源： 题型：
查看答案和解析>>【题目】抛物线y=（x﹣2）2﹣2的顶点坐标是（ ）
A.（2，﹣2）B.（﹣2，﹣2）C.（2，2）D.（﹣2，2）
-
科目： 来源： 题型：
查看答案和解析>>【题目】综合题。
（1）阅读以下内容并回答问题：
小雯用这个方法进行了尝试，点
向上平移3个单位后的对应点 
的坐标为 ， 过点 的直线的解析式为.
（2）小雯自己又提出了一个新问题请全班同学一起解答和检验此方法，请你也试试看：将直线
向右平移1个单位，平移后直线的解析式为 ， 另外直接将直线 向（填“上”或“下”）平移个单位也能得到这条直线.
（3）请你继续利用这个方法解决问题：
对于平面直角坐标系xOy内的图形M，将图形M上所有点都向上平移3个单位，再向右平移1个单位，我们把这个过程称为图形M的一次“斜平移”. 求将直线 进行两次“斜平移”后得到的直线的解析式.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点P是等边三角形ABC内一点，且PA=3，PB=4，PC=5，若将△APB绕着点B逆时针旋转后得到△CQB，则∠APB的度数 ______ ．
-
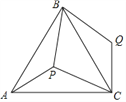
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系内，⊙C与y轴相切于D点，与x轴相交于A（2，0）、B（8，0）两点，圆心C在第四象限．
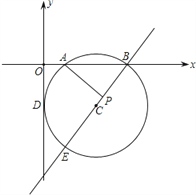
（1）求点C的坐标；
（2）连接BC并延长交⊙C于另一点E，若线段BE上有一点P，使得AB2=BPBE，能否推出AP⊥BE？请给出你的结论，并说明理由；
（3）在直线BE上是否存在点Q，使得AQ2=BQEQ？若存在，求出点Q的坐标；若不存在，也请说明理由．
相关试题
