【题目】现在的青少年由于沉迷电视、手机、网络游戏,视力日渐减退,重庆某校九年级一班班主任为了了解可能影响学生视力下降的原因,对本班进行了一个“最喜爱的娱乐”调查,每个学生在A(看电视)、B(玩手机)、C(玩网络游戏)、D(其它)四种类型中只能选一项,并根据调查结果绘制成如下两幅不完整的统计图,请根据这两幅统计图解答下列问题:
(1)扇形统计图中C所占的百分比为 ,该班学生由于玩网络游戏而视力下降的学生有 人.
(2)为了让学生深刻认识保护视力的重要性,学校组织“保护视力 健康人生”的演讲比赛,班主任从选择D类型的学生中随机抽选两名学生参加比赛.已知D类型中有女生3人,其余的为男生.请求出刚好抽到的学生全部为女生的概率.


参考答案:
【答案】(1)20%,8(2)![]()
【解析】分析:(1)用1减去A、B、D所占比例即可求解;用A(B、D)的人数除以所占比例即可得总人数,再乘以C所占比例即可;
(2)画树状图中列表法求解即可.
详解:扇形统计图中C所占的百分比为:1-10%-20%-50%=20%;
该班总人数为:4÷10%=40(人)
由于玩网络游戏而视力下降的学生数为:40×20%=8(人).
(2)列表为:
男 | 女 | 女 | 女 | |
男 | 男女 | 男女 | 男女 | |
女 | 女男 | 女女 | 女女 | |
女 | 女男 | 女女 | 女女 | |
女 | 女男 | 女女 | 女女 |
由表格知,共有12种等可能的结果,期中全部为女生的有6种,
故刚好抽到的学生全部为女生的概率为:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以直线
 上一点
上一点 为端点作射线
为端点作射线 ,使
,使 ,在同一个平面内将一个直角三角板的直角顶点放在点
,在同一个平面内将一个直角三角板的直角顶点放在点 处.(注:
处.(注: )
)(1)如图1,如果直角三角板
 的一边
的一边 放在射线
放在射线 上,那么
上,那么 的度数为______;
的度数为______;
(2)如图2,将直角三角板
 绕点
绕点 按顺时针方向转动到某个位置,如果
按顺时针方向转动到某个位置,如果 恰好平分
恰好平分 ,求
,求 的度数;
的度数;
(3)如图3,将直角三角板
 绕点
绕点 任意转动,如果
任意转动,如果 始终在
始终在 的内部,请直接用等式表示
的内部,请直接用等式表示 和
和 之间的数量关系.
之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AD//BC,AD=AB=2,∠B=120°,∠ADC=150°,现以对角线AC为边向点D一侧作等边△ACE,则四边形ABCE的面积=______.
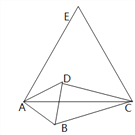
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学活动:擦出智慧的火花---------由特殊到一般的数学思想.
数学课上,李老师出示了问题:如图1,四边形ABCD是正方形,点E是边BC上的点,过点E作EF⊥AE,过点F作FG⊥BC交BC的延长线于点G..
(1)求证:∠BAE=∠FEG.
(2)同学们很快做出了解答,之后李老师将题目修改成:如图2,四边形ABCD是正方形,点E是边BC的中点.∠AEF=90°,且EF交正方形外角∠DCG的平分线于点F,求证:AE=EF.
经过思考,小明展示了一种正确的解题思路:取AB的中点M,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF.请借助图1完成小明的证明;
在(2)的基础上,同学们作了进一步的研究:
(3)小聪提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小聪的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形BFEC中,连接FC,并延长至点D,延长CF至点A,使DC=AF,连接AB、DE.
(1)求证:AB∥DE.
(2)若平行四边形BFEC是菱形,且∠ABC=90°,AB=4,BC=3,则CF= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中:
①0是最小的整数;
②有理数不是正数就是负数;
③正整数、负整数、正分数、负分数统称为有理数;
④非负数就是正数;
⑤
 不仅是有理数,而且是分数;
不仅是有理数,而且是分数;⑥
 是无限不循环小数,所以不是有理数;
是无限不循环小数,所以不是有理数;⑦无限小数不都是有理数;
⑧正数中没有最小的数,负数中没有最大的数.
其中错误的说法的个数为( )
A.7个B.6个C.5个D.4个
相关试题

