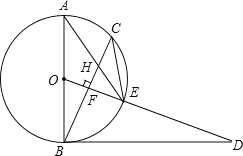
【题目】已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
(1)求证:BD是⊙O的切线;
(2)求证:CE2=EHEA;
(3)若⊙O的半径为5,sinA=![]() ,求BH的长.
,求BH的长.
参考答案:
【答案】(1)证明见解析;
(2)证明见解析;
(3)BH=![]() .
.
【解析】
试题分析:(1)由圆周角定理和已知条件证出∠ODB=∠ABC,再证出∠ABC+∠DBF=90°,即∠OBD=90°,即可得出BD是⊙O的切线;
(2)连接AC,由垂径定理得出![]() ,得出∠CAE=∠ECB,再由公共角∠CEA=∠HEC,证明△CEH∽△AEC,得出对应边成比例
,得出∠CAE=∠ECB,再由公共角∠CEA=∠HEC,证明△CEH∽△AEC,得出对应边成比例![]() ,即可得出结论;
,即可得出结论;
(3)连接BE,由圆周角定理得出∠AEB=90°,由三角函数求出BE,再根据勾股定理求出EA,得出BE=CE=6,由(2)的结论求出EH,然后根据勾股定理求出BH即可.
试题解析:(1)∵∠ODB=∠AEC,∠AEC=∠ABC,∴∠ODB=∠ABC,
∵OF⊥BC,∴∠BFD=90°,∴∠ODB+∠DBF=90°,∴∠ABC+∠DBF=90°,
即∠OBD=90°,∴BD⊥OB,∴BD是⊙O的切线;
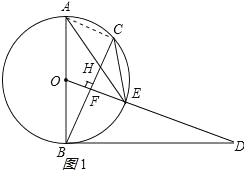
(2)连接AC,如图1所示:∵OF⊥BC,∴![]() ,
,
∴∠CAE=∠ECB,∵∠CEA=∠HEC,∴△CEH∽△AEC,
∴![]() ,
,
∴CE2=EHEA;
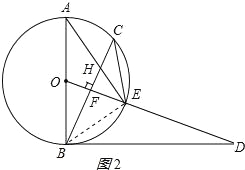
(3)连接BE,如图2所示:
∵AB是⊙O的直径,
∴∠AEB=90°,
∵⊙O的半径为5,sin∠BAE=![]() ,
,
∴AB=10,BE=ABsin∠BAE=10×![]() =6,
=6,
∴EA=![]() =8,
=8,
∵![]() ,∴BE=CE=6,∵CE2=EHEA,
,∴BE=CE=6,∵CE2=EHEA,
∴EH=![]() ,
,
在Rt△BEH中,BH=![]() =
= =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司投资某个工程项目,现在甲、乙两个工程队有能力承包这个项目.公司调查发现:乙队单独完成工程的时间是甲队的
 倍;甲、乙两队合作完成工程需要
倍;甲、乙两队合作完成工程需要 天;甲队每天的工作费用为
天;甲队每天的工作费用为 元、乙队每天的工作费用为
元、乙队每天的工作费用为 元.根据以上信息,从节约资金的角度考虑,公司应选择哪个工程队、应付工程队费用多少元?
元.根据以上信息,从节约资金的角度考虑,公司应选择哪个工程队、应付工程队费用多少元? -
科目: 来源: 题型:
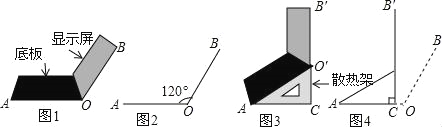
查看答案和解析>>【题目】小红将笔记本电脑水平放置在桌子上,显示屏OB与底板OA所在水平线的夹角为120°,感觉最舒适(如图1),侧面示意图为图2.使用时为了散热,她在底板下垫入散热架ACO′后,电脑转到AO′B′位置(如图3),侧面示意图为图4.已知OA=OB=24cm,O′C⊥OA于点C,O′C=12cm.
(1)求∠CAO′的度数.
(2)显示屏的顶部B′比原来升高了多少?
(3)如图4,垫入散热架后,要使显示屏O′B与水平线的夹角仍保持120°,则显示屏O′B′应绕点O′按顺时针方向旋转多少度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算x3·(-3x)2的结果是( )
A. 6x5 B. -6x5
C. 9x5 D. -9x5
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(3a-2b)·(2b+3a)=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数据4,x,-1,3的极差为6,那么x为( )
A. 5 B. -2 C. 5或-1 D. 5或-2
-
科目: 来源: 题型:
查看答案和解析>>【题目】使方程左、右两边相等的未知数的值,叫做方程的解,
x=2 (填是或不是)方程3x-8=2 的解,
写出一个方程,使它的解为2,这个方程是 .
相关试题

