【题目】小红将笔记本电脑水平放置在桌子上,显示屏OB与底板OA所在水平线的夹角为120°,感觉最舒适(如图1),侧面示意图为图2.使用时为了散热,她在底板下垫入散热架ACO′后,电脑转到AO′B′位置(如图3),侧面示意图为图4.已知OA=OB=24cm,O′C⊥OA于点C,O′C=12cm.
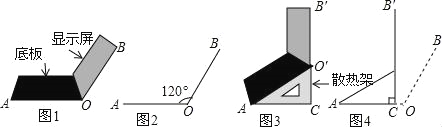
(1)求∠CAO′的度数.
(2)显示屏的顶部B′比原来升高了多少?
(3)如图4,垫入散热架后,要使显示屏O′B与水平线的夹角仍保持120°,则显示屏O′B′应绕点O′按顺时针方向旋转多少度?
参考答案:
【答案】(1)∠CAO′=30°;
(2)显示屏的顶部B′比原来升高了(36﹣12![]() )cm;
)cm;
(3)显示屏O′B′应绕点O′按顺时针方向旋转30°.
【解析】
试题分析:(1)通过解直角三角形即可得到结果;
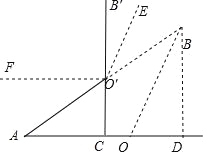
(2)过点B作BD⊥AO交AO的延长线于D,通过解直角三角形求得BD=OBsin∠BOD=24×![]() =12
=12![]() ,由C、O′、B′三点共线可得结果;
,由C、O′、B′三点共线可得结果;
(3)显示屏O′B′应绕点O′按顺时针方向旋转30°,求得∠EO′B′=∠FO′A=30°,既是显示屏O′B′应绕点O′按顺时针方向旋转30°.
试题解析:(1)∵O′C⊥OA于C,OA=OB=24cm,
∴sin∠CAO′=![]() ,
,
∴∠CAO′=30°;
(2)过点B作BD⊥AO交AO的延长线于D,∵sin∠BOD=![]() ,∴BD=OBsin∠BOD,∵∠AOB=120°,∴∠BOD=60°,∴BD=OBsin∠BOD=24×
,∴BD=OBsin∠BOD,∵∠AOB=120°,∴∠BOD=60°,∴BD=OBsin∠BOD=24×![]() =12
=12![]() ,∵O′C⊥OA,∠CAO′=30°,
,∵O′C⊥OA,∠CAO′=30°,
∴∠AO′C=60°,∵∠AO′B′=120°,∴∠AO′B′+∠AO′C=180°,
∴O′B′+O′C﹣BD=24+12﹣12![]() =36﹣12
=36﹣12![]() ,
,
∴显示屏的顶部B′比原来升高了(36﹣12![]() )cm;
)cm;
(3)显示屏O′B′应绕点O′按顺时针方向旋转30°,
理由:∵显示屏O′B与水平线的夹角仍保持120°,
∴∠EO′F=120°,
∴∠FO′A=∠CAO′=30°,
∵∠AO′B′=120°,
∴∠EO′B′=∠FO′A=30°,
∴显示屏O′B′应绕点O′按顺时针方向旋转30°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年是新中国成立70周年,是决胜全面建成小康社会第一个百年奋斗目标的关键之年,脱贫攻坚成效明显.按照现行农村贫困标准计算,2019年末农村贫困人口比上年末减少1109万人,将1109万人用科学记数法表示为________人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某药品原价是95元,经连续两次降价后,价格变为60.8元,如果每次降价的百分率是一样的,那么每次降价的百分率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司投资某个工程项目,现在甲、乙两个工程队有能力承包这个项目.公司调查发现:乙队单独完成工程的时间是甲队的
 倍;甲、乙两队合作完成工程需要
倍;甲、乙两队合作完成工程需要 天;甲队每天的工作费用为
天;甲队每天的工作费用为 元、乙队每天的工作费用为
元、乙队每天的工作费用为 元.根据以上信息,从节约资金的角度考虑,公司应选择哪个工程队、应付工程队费用多少元?
元.根据以上信息,从节约资金的角度考虑,公司应选择哪个工程队、应付工程队费用多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】计算x3·(-3x)2的结果是( )
A. 6x5 B. -6x5
C. 9x5 D. -9x5
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
(1)求证:BD是⊙O的切线;
(2)求证:CE2=EHEA;
(3)若⊙O的半径为5,sinA=
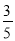 ,求BH的长.
,求BH的长.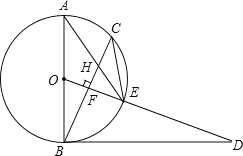
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(3a-2b)·(2b+3a)=________.
相关试题

