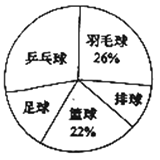
【题目】时代中学从学生兴趣出发,实施体育活动课走班制.为了了解学生最喜欢的一种球类运动,以便合理安排活动场地,在全校至少喜欢一种球类(乒乓球、羽毛球、排球、篮球、足球)运动的1200名学生中,随机抽取了若干名学生进行调查(每人只能在这五种球类运动中选择一种).调查结果统计如下:
球类名称 | 乒乓球 | 羽毛球 | 排球 | 篮球 | 足球 |
人数 | 42 |
| 15 | 33 |
|
解答下列问题:
(1)这次抽样调查中的样本是________;
(2)统计表中,![]() ________,
________,![]() ________;
________;
(3)试估计上述1200名学生中最喜欢乒乓球运动的人数.
参考答案:
【答案】(1)时代中学学生最喜欢的一种球类运动情况;(2)39,21;(3)336人.
【解析】分析: (1)直接利用样本的定义分析得出答案;
(2)用喜欢排球的人数除以其所占的百分比即可求得样本容量,用样本容量乘以羽毛球所占的百分比即可求得a,用样本容量减去其他求得b值;
(3)用总人数乘以喜欢乒乓球的人所占的百分比即可.
详解:
(1)这次抽样调查中的样本是:时代中学学生最喜欢的一种球类运动情况;
故答案为:时代中学学生最喜欢的一种球类运动情况;
(2)∵喜欢蓝球的有33人,占22%,
∴样本容量为33÷22%=150;
a=150×26%=39(人),
b=150-39-42-15-33=21(人);
故答案为:39,21;
(3)最喜欢乒乓球运动的人数为:1200×![]() =336(人).
=336(人).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市预测某饮料有发展前途,用1600元购进一批饮料,面市后果然供不应求,又用6000元购进这批饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若二次购进饮料按同一价格销售,两批全部售完后,获利不少于1200元,那么销售单价至少为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一条不完整的数轴上从左到右有
 三个点,其中点
三个点,其中点 到点
到点 的距离为3,点
的距离为3,点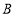 到
到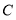 的距离为4设点
的距离为4设点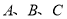 所对应的数的和是
所对应的数的和是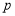

(1)若以
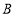 为原点,写出点
为原点,写出点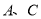 所对应的数,并计算
所对应的数,并计算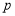 的值;若以
的值;若以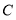 为原点,求
为原点,求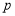 的值;
的值;(2)若原点
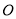 在图中数轴上点
在图中数轴上点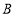 的左侧,且点
的左侧,且点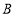 到原点
到原点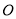 的距离为1,求
的距离为1,求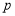 的值;
的值;(3)若原点
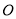 在图中数轴上点
在图中数轴上点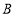 的右侧,且点
的右侧,且点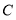 到点
到点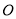 的距离为
的距离为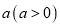 ,求
,求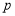 的值(用含
的值(用含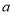 的式子表示)
的式子表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F,作CM⊥AD,垂足为M,下列结论不正确的是( )

A. AD=CE B. MF=
 CF C. ∠BEC=∠CDA D. AM=CM
CF C. ∠BEC=∠CDA D. AM=CM -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
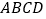 中,
中, 是
是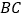 上的一点,连接
上的一点,连接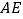 ,过
,过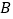 点作
点作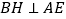 ,垂足为点
,垂足为点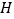 ,延长
,延长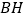 交
交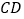 于点
于点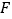 ,连接
,连接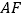 .
.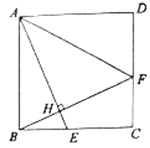
(1)求证:
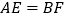 .
.(2)若正方形边长是5,
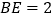 ,求
,求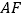 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,给出五个等量关系:①AD=BC;②AC=BD;③CE=DE;④∠D=∠C;⑤∠DAB=∠CBA.
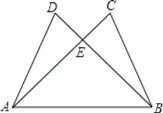
请你以其中两个为条件,另外三个中的一个为结论,推出一个正确的结论(只需写出一种情况),并加以证明.
已知:
求证:
证明:
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点M为直线AB上一动点,
 都是等边三角形,连接BN
都是等边三角形,连接BN  求证:
求证:  ;
; 分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系
分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系 不需证明
不需证明 ;
; 如图4,当
如图4,当 时,证明:
时,证明:  .
.
相关试题

