【题目】如图,现有一个均匀的转盘被平均分成6等份,分别标有数字2、3、4、5、6、7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字.

求:(1)转动转盘,转出的数字大于3的概率是多少?
(2)现有两张分别写有3和4的卡片,随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.
①这三条线段能构成三角形的概率是 .
②这三条线段能构成等腰三角形的概率是 .
参考答案:
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() .
.
【解析】
(1)转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,大于3的结果有4种,由概率公式可得;
(2)①转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,能够成三角形的结果有5种,由概率公式可得;
②转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,能够成等腰三角形的结果有2种,由概率公式可得.
解: (1)转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,大于3的结果有4种,
∴转出的数字大于3的概率是![]()
(2)①转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,能够成三角形的结果有5种,
∴这三条线段能构成三角形的概率是![]()
②转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,能够成等腰三角形的结果有2种,
∴这三条线段能构成等腰三角形的概率是![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】古代阿拉伯数学家泰比特·伊本·奎拉对勾股定理进行了推广研究:如图(图1中
 为锐角,图2中
为锐角,图2中 为直角,图3中
为直角,图3中 为钝角).
为钝角).
在△ABC的边BC上取
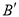 ,
,  两点,使
两点,使 ,则
,则 ∽
∽ ∽
∽ ,
,  ,
, 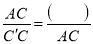 ,进而可得
,进而可得
 ;(用
;(用 表示)
表示)若AB=4,AC=3,BC=6,则

 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,函数
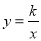 (x<0)与y=ax+b的图象交于点A(﹣1,n)和点B(﹣2,1).
(x<0)与y=ax+b的图象交于点A(﹣1,n)和点B(﹣2,1).(1)求k,a,b的值;
(2)直线x=m与
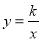 (x<0)的图象交于点P,与y=﹣x+1的图象交于点Q,当∠PAQ>90°时,直接写出m的取值范围.
(x<0)的图象交于点P,与y=﹣x+1的图象交于点Q,当∠PAQ>90°时,直接写出m的取值范围.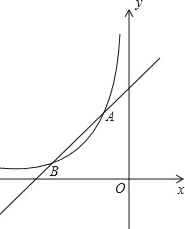
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中,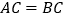 ,
, ,
, 平分
平分 ,
,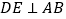 于
于 ,则下列结论:①
,则下列结论:① 平分
平分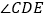 ,②
,②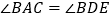 ,③
,③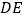 平分
平分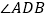 ,④
,④ ,其中正确的有( )
,其中正确的有( )
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,
①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
②若点P、Q的运动路程分别为a、b(单位:cm,ab≠0),已知A、C、P、Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B,C三点在⊙O上,直径BD平分∠ABC,过点D作DE∥AB交弦BC于点E,在BC的延长线上取一点F,使得EF
 DE.
DE.(1)求证:DF是⊙O的切线;
(2)连接AF交DE于点M,若 AD
 4,DE
4,DE 5,求DM的长.
5,求DM的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是某班体育考试跳绳项目模拟考试时10名同学的测试成绩(单位:个/分钟)
成绩(个/分钟)
140
160
169
170
177
180
人数
1
1
1
2
3
2
则关于这10名同学每分钟跳绳的测试成绩,下列说法错误的是( )
A.方差是135B.平均数是170C.中位数是173.5D.众数是177
相关试题

