【题目】如图,在ABCD中,点E,F分别在边DC,AB上,DE=BF,把平行四边形沿直线EF折叠,使得点B,C分别落在B′,C′处,线段EC′与线段AF交于点G,连接DG,B′G. 
求证:
(1)∠1=∠2;
(2)DG=B′G.
参考答案:
【答案】
(1)证明:∵在平行四边形ABCD中,DC∥AB,
∴∠2=∠FEC,
由折叠得:∠1=∠FEC,
∴∠1=∠2
(2)证明:∵∠1=∠2,
∴EG=GF,
∵AB∥DC,
∴∠DEG=∠EGF,
由折叠得:EC′∥B′F,
∴∠B′FG=∠EGF,
∵DE=BF=B′F,
∴DE=B′F,
∴△DEG≌△B′FG(SAS),
∴DG=B′G.
【解析】(1)根据平行四边形得出DC∥AB,推出∠2=∠FEC,由折叠得出∠1=∠FEC=∠2,即可得出答案;(2)求出EG=B′G,推出∠DEG=∠EGF,由折叠求出∠B′FG=∠EGF,求出DE=B′F,证△DEG≌△B′FG即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学有一块四边形的空地ABCD,如图所示,为了绿化环境,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m.
(1)求出空地ABCD的面积.
(2)若每种植1平方米草皮需要200元,问总共需投入多少元?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A在反比例函数y=﹣
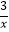 (x<0)的图象上移动,连接OA,作OB⊥OA,并满足∠OAB=30°.在点A的移动过程中,追踪点B形成的图象所对应的函数表达式为( )
(x<0)的图象上移动,连接OA,作OB⊥OA,并满足∠OAB=30°.在点A的移动过程中,追踪点B形成的图象所对应的函数表达式为( ) 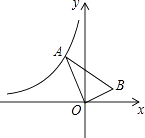
A.y=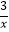 (x>0)
(x>0)
B.y=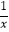 (x>0)
(x>0)
C.y=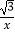 (x>0)
(x>0)
D.y=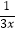 (x>0)
(x>0) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E为AD的中点,连接EC,过点E作EF⊥EC,交AB于点F,则tan∠ECF= .

-
科目: 来源: 题型:
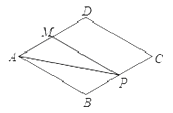
查看答案和解析>>【题目】如图,菱形ABCD中,AB=2,∠B=120°,点M是AD的中点,点P由点A出发,沿A→B→C→D作匀速运动,到达点D停止,则△APM的面积y与点P经过的路程x之间的函数关系的图象大致是( )
A.
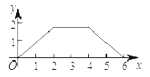 B.
B. 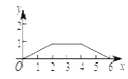 C.
C. 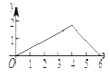 D.
D. 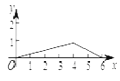
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知直线l:y=﹣x+2与y轴交于点A,抛物线y=(x﹣1)2+k经过点A,其顶点为B,另一抛物线y=(x﹣h)2+2﹣h(h>1)的顶点为D,两抛物线相交于点C.

(1)求点B的坐标,并说明点D在直线l上的理由;
(2)设交点C的横坐标为m.
交点C的纵坐标可以表示为:或;
(3)如图2,若∠ACD=90°,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”.

(1)请用直尺和圆规画一个“好玩三角形”;
(2)如图在Rt△ABC中,∠C=90°,tanA= ,求证:△ABC是“好玩三角形”;
,求证:△ABC是“好玩三角形”;
(3)如图2,已知菱形ABCD的边长为a,∠ABC=2β,点P,Q从点A同时出发,以相同速度分别沿折线AB﹣BC和AD﹣DC向终点C运动,记点P经过的路程为s.
①当β=45°时,若△APQ是“好玩三角形”,试求 的值;
的值;
②当tanβ的取值在什么范围内,点P,Q在运动过程中,有且只有一个△APQ能成为“好玩三角形”.请直接写出tanβ的取值范围.
(4)(本小题为选做题)
依据(3)的条件,提出一个关于“在点P,Q的运动过程中,tanβ的取值范围与△APQ是‘好玩三角形’的个数关系”的真命题(“好玩三角形”的个数限定不能为1)
相关试题

