【题目】已知,如图1,在 ![]() 中,AC=BC,点D是边AB的中点,E,F分别是AC和BC的中点,分别以CE,CF为一边向上作两个全等的矩形CEGH和矩形CFMN(其中EG=FM),依次连结DG、DM、GM。
中,AC=BC,点D是边AB的中点,E,F分别是AC和BC的中点,分别以CE,CF为一边向上作两个全等的矩形CEGH和矩形CFMN(其中EG=FM),依次连结DG、DM、GM。
(1)求证: ![]() 是等腰三角形。
是等腰三角形。
(2)如图2,若将上图中的两个全等的矩形改为两个全等的正三角形( ![]() 和
和 ![]() ),其他条件不变。请探究
),其他条件不变。请探究 ![]() 的形状,并说明理由。
的形状,并说明理由。
(3)若将上图中的两个全等的矩形改为两个正方形,并把 ![]() 中的边BC缩短到如图3形状,请探究
中的边BC缩短到如图3形状,请探究 ![]() 的形状,并说明理由。
的形状,并说明理由。
参考答案:
【答案】
(1)
证明:∵四边形CEGH和CFMN是全等的矩形,
∴CE=CF,EG=FM,∠GEC=∠MFC= 90°.
连接DE、DF,如图1.

∵D、E、F分别是AB、AC、BC的中点,
∴DE∥BC,且DE=CF=![]() BC;
BC;
DF∥AC,且DF=CE=![]() AC.
AC.
∴四边形DECF是平行四边形.
∴ ∠DEC=∠DFC.
又∵∠GEC=∠MFC,∴∠DEG=∠DFM.
∵AC=BC,∴DE=DF.
∴△DEG ≌ △DFM(SAS).
∴DG=DM.
∴△DGM是等腰三角形.
(2)
解:△DGM是等边三角形.
证明:∵△CEG和△CFM是全等的等边三角形,
∴CE =EG =CG=CF=FM=CM,∠GEC =∠MFC = 60°.
连接DE、DF,如图2.
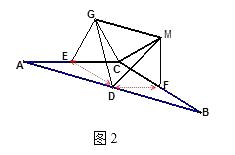
∵D、E、F分别是AB、AC、BC的中点,
∴DE∥BC,且DE = CF
=![]() BC,DF∥AC,且DF = CE =
BC,DF∥AC,且DF = CE =![]() AC.
AC.
∴四边形DECF是平行四边形.
∴ ∠DEC =∠DFC.
又∵∠GEC =∠MFC,∴∠DEG=∠DFM.
∵AC=BC,∴DE=DF.
∴△DEG ≌ △DFM(SAS).
∴DG=DM.
∴△DGM是等腰三角形.
又∵∠GCM+∠ACB=360°-60°-60°=240°
∠GED+∠ACB=∠GEC+∠CED+∠ACB=60°+180°=240°
∴∠GCM=∠GED
又DE=CF=CM,EG=CG
∴△GED≌ △GCM(SAS).
∴GM=GD
∴△DGM是等边三角形.
(3)
解:△DGM是等腰直角三角形.

显然,由(1)(2)易得△DEG≌ △MFD(SAS)
∴DG=DM,∠DGE=∠MDF
∵DF∥AC
∴∠CED+∠EDF=180°
即:∠CED+∠EDG+∠GDM+∠MDF=180°
又由三角形内角和可知∠CED+∠EDG+∠GEC+∠DGE=180°
∴∠GDM=∠GEC=90°
∴△DGM是等腰直角三角形.
【解析】三个小题都要证明△DFM≌ △DFM(SAS),证明方法类似;再根据全等的性质和每小题的不同点证明得到答案.
【考点精析】本题主要考查了三角形中位线定理和矩形的性质的相关知识点,需要掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;矩形的四个角都是直角,矩形的对角线相等才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一扇窗户垂直打开,即OM⊥OP , AC是长度不变的滑动支架,其中一端固定在窗户的点A处,另一端C在OP上滑动,将窗户OM按图示方向向内旋转37°到达ON位置,此时,点A、C的对应位置分别是点B、D.测量出∠ODB为28°,点D到点O的距离为30cm .

(1)求B点到OP的距离;
(2)求滑动支架的长.(结果精确到0.1)(数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53,sin 53°≈0.8,cos53°≈0.6,tan53°≈1.33) -
科目: 来源: 题型:
查看答案和解析>>【题目】随着互联网、移动终端的迅速发展,数字化阅读越来越普及,公交上的“低头族”越来越多.某研究机构针对“您如何看待数字化阅读”问题进行了随机问卷调查(如图1),并将调查结果绘制成图2和图3所示的统计图(均不完整).
请根据统计图中提供的信息,解答下列问题:


(1)求出本次接受调查的总人数,并将条形
统计图补充完整;
(2)表示观点B的扇形的圆心角度数为度;
(3)若嘉兴市人口总数约为270万,请根据图中信息,估计湖州市民认同观点D的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】嘉兴教育学院大学生小王利用暑假开展了30天的社会实践活动,参与了嘉兴浙北超市的经营,了解到某成本为15元/件的商品在x天销售的相关信息,如表表示:
销售量p(件)
P=45﹣x
销售单价q(元/件)
当1≤x≤18时,q=20+x
当18<x≤30时,q=38设该超市在第x天销售这种商品获得的利润为y元.
(1)求y关于x的函数关系式;
(2)在这30天中,该超市销售这种商品第几天的利润最大?最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,将矩形OABC置于平面直角坐标系中,点A,C分别在x,y轴的正半轴上,已知点B(4,2),将矩形OABC翻折,使得点C的对应点P恰好落在线段OA(包括端点O,A)上,折痕所在直线分别交BC、OA于点D、E;若点P在线段OA上运动时,过点P作OA的垂线交折痕所在直线于点Q.

(1)求证:CQ=QP
(2)设点Q的坐标为(x,y),求y关于x的函数关系式及自变量x的取值范围;
(3)如图2,连结OQ,OB,当点P在线段OA上运动时,设三角形OBQ的面积为S,当x取何值时,S取得最小值,并求出最小值;
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式组
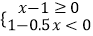 的最小整数解是( )
的最小整数解是( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B、C重合),现将△PCD沿直线PD折叠,使点C落到点C’处;作∠BPC’的角平分线交AB于点E . 设BP=x , BE=y , 则下列图象中,能表示y与x的函数关系的图象大致是( )

A.
B.
C.
D.
相关试题

