【题目】(本题满分8分)我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)计算两队决赛成绩的平均数;
(2)计算两队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.
参考答案:
【答案】(1)初中部平均数为:85,高中部平均数为:85;(2)初中代表队手成绩较为稳定.
【解析】
试题分析:(1)分别求出初中、高中部的平均数即可;
(2)分别求出初中、高中部的方差即可.
试题解析:(1)初中部平均数为:(75+80+85+85+100)÷5=85(分),
高中部平均数为:(70+100+100+75+80)÷5=85(分);
(2)∵![]()
![]() [(75﹣85)2+(80﹣85)2+(85﹣85)2+(85﹣85)2+ (100﹣85)2]=70,
[(75﹣85)2+(80﹣85)2+(85﹣85)2+(85﹣85)2+ (100﹣85)2]=70,
![]()
![]() [(70﹣85)2+(100﹣85)2+(100﹣85)2+(75﹣85)2+(80﹣85)2]=160,
[(70﹣85)2+(100﹣85)2+(100﹣85)2+(75﹣85)2+(80﹣85)2]=160,
∴![]() <
<![]() ,因此,初中代表队选手成绩较为稳定.
,因此,初中代表队选手成绩较为稳定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题:(用简便方法计算)
(1)-102n×100×(-10)2n-1; (2)[(-a)(-b)2a2b3c]2;
(3)(x3)2÷x2÷x+x3÷(-x)2(-x2); (4)(-9)3×( -
 )3
)3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE⊥AD,交AB于点E,AE为⊙O的直径

(1)判断BC与⊙O的位置关系,并证明你的结论;
(2)求证:△ABD∽△DBE;
(3)若cosB= ,AE=4,求CD.
,AE=4,求CD. -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下列各题:
(1)计算:-22+|5-8|+24÷(-3)×
 ;
;(2)化简与计算:
①化简:3x2-[7x-(4x-3)-2x2];
②先化简,再求值:
 x-2
x-2 +
+ ,其中x=-2,y=
,其中x=-2,y= ;
;(3)解方程:
①32x-64=16x+32;
②-
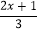 =2-
=2-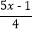 .
. -
科目: 来源: 题型:
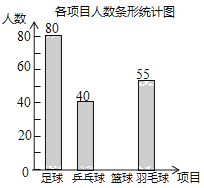
查看答案和解析>>【题目】某学校准备开展“阳光体育活动”,决定开设以下体育活动项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择一项,为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并将通过获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据统计图回答问题:
(1)这次活动一共调查了 名学生;
(2)补全条形统计图;
(3)在扇形统计图中,选择篮球项目的人数所在扇形的圆心角等于 度;
(4)若该学校有1500人,请你估计该学校选择足球项目的学生人数约是 人。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,直线y=
 x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
(1)求抛物线F1所表示的二次函数的表达式;
(2)若点M是抛物线F1位于第二象限图象上的一点,设四边形MAOC和△BOC的面积分别为S四边形MAOC和S△BOC , 记S=S四边形MAOC﹣S△BOC , 求S最大时点M的坐标及S的最大值;
(3)如图②,将抛物线F1沿y轴翻折并“复制”得到抛物线F2 , 点A、B与(2)中所求的点M的对应点分别为A′、B′、M′,过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.
相关试题

