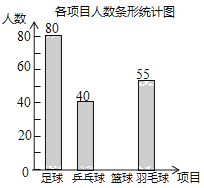
【题目】某学校准备开展“阳光体育活动”,决定开设以下体育活动项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择一项,为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并将通过获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据统计图回答问题:
(1)这次活动一共调查了 名学生;
(2)补全条形统计图;
(3)在扇形统计图中,选择篮球项目的人数所在扇形的圆心角等于 度;
(4)若该学校有1500人,请你估计该学校选择足球项目的学生人数约是 人。

参考答案:
【答案】(1)250;(2)条形图见解析;(3)108;(4)480.
【解析】试题分析:(1)由喜欢足球的人数除以所占的百分比即可求出总人数;
(2)由总人数减去喜欢足球、乒乓球、羽毛球的人数,即可求出喜欢篮球C的人数,补全统计图即可;(3)用360乘以选择篮球项目的人数所占的百分比即可;(4)用1500乘以喜欢足球的人数所占的百分比即可得该学校选择足球项目的学生人数.
试题解析:
(1) 根据题意得:80÷32%=250(人),
则这次被调查的学生共有250人;
(2)喜欢篮球的人数为:250-80-75-55=40(人),补全统计图如下:

(3)360×![]() =108°.
=108°.
(4)1500×32%=480(人)
∴该学校选择足球项目的学生人数约是480人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE⊥AD,交AB于点E,AE为⊙O的直径

(1)判断BC与⊙O的位置关系,并证明你的结论;
(2)求证:△ABD∽△DBE;
(3)若cosB= ,AE=4,求CD.
,AE=4,求CD. -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下列各题:
(1)计算:-22+|5-8|+24÷(-3)×
 ;
;(2)化简与计算:
①化简:3x2-[7x-(4x-3)-2x2];
②先化简,再求值:
 x-2
x-2 +
+ ,其中x=-2,y=
,其中x=-2,y= ;
;(3)解方程:
①32x-64=16x+32;
②-
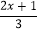 =2-
=2-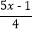 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分8分)我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)计算两队决赛成绩的平均数;
(2)计算两队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,直线y=
 x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
(1)求抛物线F1所表示的二次函数的表达式;
(2)若点M是抛物线F1位于第二象限图象上的一点,设四边形MAOC和△BOC的面积分别为S四边形MAOC和S△BOC , 记S=S四边形MAOC﹣S△BOC , 求S最大时点M的坐标及S的最大值;
(3)如图②,将抛物线F1沿y轴翻折并“复制”得到抛物线F2 , 点A、B与(2)中所求的点M的对应点分别为A′、B′、M′,过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(7分)某学校举行演讲比赛,选出了10名同学担任评委,并事先拟定从如下4个方案中选择合理的方案来确定每个演讲者的最后得分(满分为10分):
方案1:所有评委所给分的平均数,
方案2:在所有评委所给分中,去掉一个最高分和一个最低分.然后再计算其余给分的l平均数.
方案3:所有评委所给分的中位效.
方案4:所有评委所给分的众数.
为了探究上述方案的合理性.先对某个同学的演讲成绩进行了统计实验.下面是这个同学的得分统计图:

(1)分别按上述4个方案计算这个同学演讲的最后得分;
(2)根据(1)中的结果,请用统计的知识说明哪些方案不适台作为这个同学演讲的最后得分,并给出该同学的最后得分.
相关试题

