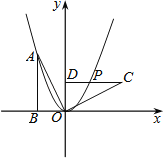
【题目】如图,Rt△OAB的顶点A(﹣2,4)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为( )
A.(![]() ,
,![]() ) B.(2,2) C.(
) B.(2,2) C.(![]() ,2) D.(2,
,2) D.(2,![]() )
)
参考答案:
【答案】C
【解析】
试题分析:首先根据点A在抛物线y=ax2上求得抛物线的解析式和线段OB的长,从而求得点D的坐标,根据点P的纵坐标和点D的纵坐标相等得到点P的坐标即可;
解:∵Rt△OAB的顶点A(﹣2,4)在抛物线y=ax2上,
∴4=a×(﹣2)2,
解得:a=1
∴解析式为y=x2,
∵Rt△OAB的顶点A(﹣2,4),
∴OB=OD=2,
∵Rt△OAB绕点O顺时针旋转90°,得到△OCD,
∴CD∥x轴,
∴点D和点P的纵坐标均为2,
∴令y=2,得2=x2,
解得:x=±![]() ,
,
∵点P在第一象限,
∴点P的坐标为:(![]() ,2)
,2)
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a+a2=a3
B.(a2)3=a6
C.(x﹣y)2=x2﹣y2
D.a2a3=a6 -
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数按要求填入相应的大括号里:
-10,4.5,-
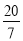 , 0,-(-3),2.10010001…,-π,
, 0,-(-3),2.10010001…,-π,整数集合:{ },分数集合:{ },
正有理数集合:{ },无理数集合:{ }.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)(﹣6)+(+8)﹣(+4)﹣(﹣2)
(2)(﹣7)×(﹣5)﹣90÷(﹣15)
(3)(
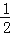 ﹣
﹣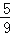 +
+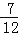 )×(﹣36)
)×(﹣36)(4)2÷(﹣
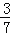 )×
)×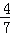 ÷(﹣
÷(﹣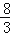 )
)(5)﹣24+(4﹣9)2﹣5×(﹣1)6
(6)用简便方法计算:(﹣370)×(﹣
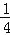 )+0.25×24.5﹣5
)+0.25×24.5﹣5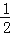 ×(﹣25%)
×(﹣25%) -
科目: 来源: 题型:
查看答案和解析>>【题目】适合下列条件的△ABC中,直角三角形的个数为( )
①a=
 ,b=
,b=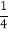 ,c=
,c=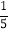 ; ②a=6,b=8,c=10; ③a=7,b=24,c=25;
; ②a=6,b=8,c=10; ③a=7,b=24,c=25;④a=2,b=3,c=4.
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,LA,LB分别表示A步行与B骑车在同一路上行驶的路程y(千米)与时间x(小时)的关系.根据图象,回答下列问题:

(1)B出发时与A相距 千米.
(2)B骑车一段路后,自行车发生故障,进行修理,所用的时间是 小时.
(3)B出发后 小时与A相遇.
(4)求出A行走的路程y与时间x的函数关系式.(写出过程)
(5)若B的自行车不发生故障,保持出发时的速度匀速行驶,A,B肯定会提前相遇.在图中画出这种假设情况下B骑车行驶过程中路程y与时间x的函数图象,在图中标出这个相遇点P,并回答相遇点P离B的出发点O相距多少千米.(写出过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B分别表示的数是6、﹣12,M、N、P为数轴上三个动点,它们同时都向右运动.点M从点A出发,速度为每秒2个单位长度,点N从点B出发,速度为点M的3倍,点P从原点出发,速度为每秒1个单位长度.

(1)当运动3秒时,点M、N、P分别表示的数是 、 、 ;
(2)求运动多少秒时,点P到点M、N的距离相等?
相关试题

