【题目】如图,LA,LB分别表示A步行与B骑车在同一路上行驶的路程y(千米)与时间x(小时)的关系.根据图象,回答下列问题:

(1)B出发时与A相距 千米.
(2)B骑车一段路后,自行车发生故障,进行修理,所用的时间是 小时.
(3)B出发后 小时与A相遇.
(4)求出A行走的路程y与时间x的函数关系式.(写出过程)
(5)若B的自行车不发生故障,保持出发时的速度匀速行驶,A,B肯定会提前相遇.在图中画出这种假设情况下B骑车行驶过程中路程y与时间x的函数图象,在图中标出这个相遇点P,并回答相遇点P离B的出发点O相距多少千米.(写出过程)
参考答案:
【答案】(1)10千米;(2)1小时;(3)3小时时相遇;(4)y=5x+10;(5)P(1,15),所以相遇点P离B的出发点O相距15千米.
【解析】
试题分析:(1)从图上可看出B出发时与A相距10千米.
(2)修理的时间就是路程不变的时间是1.5﹣0.5=1小时.
(3)从图象看出3小时时,两个图象相交,所以3小时时相遇.
(4)y和x的函数关系是一次函数,设函数是为y=kx+t,过(0,10)和(3,22.5),从而可求出关系式.
(5)不发生故障时,B的行走的路程和时间是正比例关系,设函数式为y=kx,过(0.5,7.5)点,求出函数式,从而求出相遇的时间.
解:(1)B出发时与A相距10千米;
(2)修理自行车的时间为:1.5﹣05=1小时;
(3)3小时时相遇;
(4)设函数是为y=kx+t,且过(0,10)和(3,25),
∴![]() ,
,
∴![]() .
.
∴y=5x+10;
(5)如图所示,设B修车前的关系式为:y=kx,过(0.5,7.5)点.
∴7.5=0.5k
∴k=15.
∴B骑车行驶过程中路程y与时间x的解析式为y=15x,
解![]() 得:
得:![]() ,
,
∴P(1,15),所以相遇点P离B的出发点O相距15千米.
故答案为:10,1,3.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)(﹣6)+(+8)﹣(+4)﹣(﹣2)
(2)(﹣7)×(﹣5)﹣90÷(﹣15)
(3)(
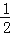 ﹣
﹣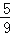 +
+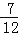 )×(﹣36)
)×(﹣36)(4)2÷(﹣
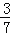 )×
)×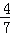 ÷(﹣
÷(﹣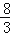 )
)(5)﹣24+(4﹣9)2﹣5×(﹣1)6
(6)用简便方法计算:(﹣370)×(﹣
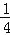 )+0.25×24.5﹣5
)+0.25×24.5﹣5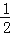 ×(﹣25%)
×(﹣25%) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△OAB的顶点A(﹣2,4)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为( )
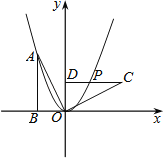
A.(
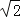 ,
,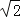 ) B.(2,2) C.(
) B.(2,2) C.(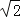 ,2) D.(2,
,2) D.(2,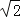 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】适合下列条件的△ABC中,直角三角形的个数为( )
①a=
 ,b=
,b=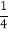 ,c=
,c=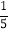 ; ②a=6,b=8,c=10; ③a=7,b=24,c=25;
; ②a=6,b=8,c=10; ③a=7,b=24,c=25;④a=2,b=3,c=4.
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B分别表示的数是6、﹣12,M、N、P为数轴上三个动点,它们同时都向右运动.点M从点A出发,速度为每秒2个单位长度,点N从点B出发,速度为点M的3倍,点P从原点出发,速度为每秒1个单位长度.

(1)当运动3秒时,点M、N、P分别表示的数是 、 、 ;
(2)求运动多少秒时,点P到点M、N的距离相等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】请将命题“等角的余角相等”改写成 “如果……那么……”的形式是_______________
-
科目: 来源: 题型:
查看答案和解析>>【题目】一种药品在进价上加价100%作为原价,后经两次降价后利润率为28%,求平均每次的降价率?
相关试题

