【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=35°,以C为旅转中心,将△ABC旋转到△A′B′C的位置,点B在边A′B′上,则∠BDC为( )
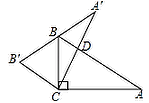
A.70°B.90°C.100°D.105°
参考答案:
【答案】D
【解析】
根据三角形内角和定理求出∠ABC,再由旋转的性质可知BC=B′C, ∠ABC=∠B′,从而求出∠BCB′,根据旋转角相等求出∠ACA′,最后根据外角定理即可求出∠BDC.
∵在Rt△ABC中,∠ACB=90°,∠A=35°,
∴∠ABC=90°-35°=55°,
由旋转的性质可知BC=B′C, ∠ABC=∠B′,∠BCB′=∠ACA′,
∴∠ABC=∠B′=∠B′BC=55°,
∴∠BCB′=180°-∠B′-∠B′BC=180°-55°-55°=70°,
∴∠ACA′=70°,
∴∠BDC=∠A+∠ACA′=35°+70°=105°.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示、方格纸中每个小正方的边长都是单位1,△ABC在平面直角坐标系中的位置图所示.
(1)将△ABC向右平移4个单位后得到△A
 B
B C
C ,请画出△A
,请画出△A B
B C
C ,并直接写出点C
,并直接写出点C 的坐标;
的坐标;(2)作出△A
 B
B C
C 关于x轴的对称图形△A
关于x轴的对称图形△A B
B C
C ,并直接写出点A
,并直接写出点A 的坐标;
的坐标;(3)请由图形直接判断以点C
 、C
、C 、B
、B 、B
、B ,为顶点的四边形是什么四边形?并求出它的面积.
,为顶点的四边形是什么四边形?并求出它的面积.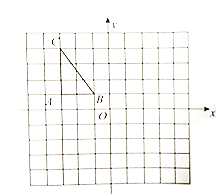
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:如果
 ,
, 是一元二次方程
是一元二次方程 的两根,那么有
的两根,那么有 ,
, .这是一元二次方程根与系数的关系,我们利用它可以用来解题,例
.这是一元二次方程根与系数的关系,我们利用它可以用来解题,例 ,
, 是方程
是方程 的两根,求
的两根,求 的值.解法可以这样:
的值.解法可以这样:∵
 ,
, ,则
,则 .
.请你根据以上解法解答下题:
已知
 ,
, 是方程
是方程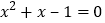 的两根,求:
的两根,求: 的值;
的值; 的值.
的值. 试求
试求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】要建一个如图所示的面积为300
 的长方形围栏,围栏总长50m,一边靠墙(墙长25m),
的长方形围栏,围栏总长50m,一边靠墙(墙长25m),
(1)求围栏的长和宽;
(2)能否围成面积为400
 的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。
的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
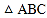 中,
中,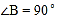 ,
,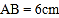 ,
,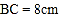 .
.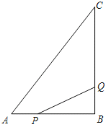
 点
点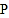 从点
从点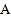 开始沿
开始沿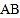 边向
边向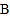 以
以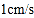 的速度移动,点
的速度移动,点 从
从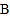 点开始沿
点开始沿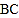 边向点
边向点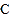 以
以 的速度移动.如果
的速度移动.如果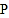 、
、 分别从
分别从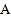 ,
,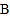 同时出发,线段
同时出发,线段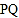 能否将
能否将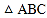 分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
分成面积相等的两部分?若能,求出运动时间;若不能说明理由. 若
若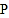 点沿射线
点沿射线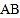 方向从
方向从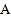 点出发以
点出发以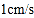 的速度移动,点
的速度移动,点 沿射线
沿射线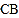 方向从
方向从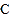 点出发以
点出发以 的速度移动,
的速度移动, 、
、 同时出发,问几秒后,
同时出发,问几秒后,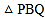 的面积为
的面积为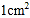 ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】对于一元二次方程
 ,下列说法:①若
,下列说法:①若 ,则方程必有一根为
,则方程必有一根为 ;②若
;②若 是方程
是方程 的一个根,则一定有
的一个根,则一定有 成立;③若
成立;③若 ,则方程
,则方程 一定有两个不相等实数根;其中正确结论有( )个.
一定有两个不相等实数根;其中正确结论有( )个.A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有长为
 的篱笆,一面利用墙(墙的最大可用长度为
的篱笆,一面利用墙(墙的最大可用长度为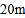 ),围成中间隔有一道篱笆(平行于
),围成中间隔有一道篱笆(平行于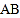 )的矩形花圃
)的矩形花圃 .设花圃的一边
.设花圃的一边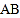 为
为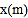 .
.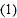 则
则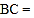 ________(用含
________(用含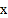 的代数式表示),矩形
的代数式表示),矩形 的面积
的面积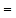 ________(用含
________(用含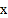 的代数式表示);
的代数式表示); 如果要围成面积为
如果要围成面积为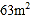 的花圃,
的花圃,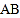 的长是多少?
的长是多少? 将
将 中表示矩形
中表示矩形 的面积的代数式通过配方,问:当
的面积的代数式通过配方,问:当 等于多少时,能够使矩形花圃
等于多少时,能够使矩形花圃 面积最大,最大的面积为多少?
面积最大,最大的面积为多少?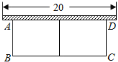
相关试题

