搜索
【题目】如图，面积为24的正方形ABCD中，有一个小正方形EFGH，其中E、F、G分别在AB、BC、FD上．若BF= 
，则小正方形的周长为（ ）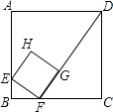 
A.
B.
C.
D.
参考答案：
【答案】C
【解析】解：∵四边形ABCD是正方形，面积为24， ∴BC=CD=2 
，∠B=∠C=90°，
∵四边形EFGH是正方形，
∴∠EFG=90°，
∵∠EFB+∠DFC=90°，∠BEF+∠EFB=90°，
∴∠BEF=∠DFC，∵∠EBF=∠C=90°，
∴△BEF∽△CFD，
∴ 
= 
，
∵BF= 
，CF= 
，DF= 
= 
，
∴ 
= 
，
∴EF= 
，
∴正方形EFGH的周长为 ．
故选C．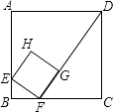
先利用勾股定理求出DF，再根据△BEF∽△CFD，得 = 求出EF即可解决问题．
-
科目： 来源： 题型：
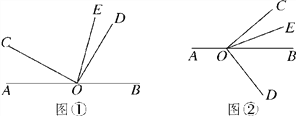
查看答案和解析>>【题目】已知O是直线AB上的一点，∠COD是直角，OE平分∠BOC.
（1）如图①，若∠AOC＝30°，求∠DOE的度数；
（2）在图①中，若∠AOC＝
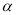，直接写出∠DOE的度数（用含
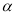的代数式表示）；（3）将图①中的∠DOC绕顶点O顺时针旋转至图②的位置，探究∠AOC和∠DOE的度数之间的关系，写出你的结论，并说明理由；
-
科目： 来源： 题型：
查看答案和解析>>【题目】根据解答过程填空（写出推理理由或根据）：
如图，已知∠DAF=∠F，∠B=∠D，试说明AB//DC
证明∵∠DAF=∠F（ 已知）
∴AD∥BF ( )
∴∠D=∠DCF( )
∵∠B=∠D( )
∴∠ =∠DCF（等量代换）
∴AB//DC( )
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y=2x+3与x轴相交于点A，与y轴相交于点B.
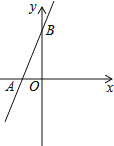
（1）求A，B两点的坐标；
（2）过B点作直线BP与x轴相交于P，且使OP=2OA， 求直线BP的解析式.
-
科目： 来源： 题型：
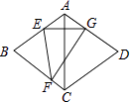
查看答案和解析>>【题目】如图，在菱形ABCD中，∠BAD=120°，将菱形沿EF折叠，点B正好落在AD边的点G处，且EG⊥AC，若CD=8，则FG的长为（ ）
A.4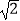
B.4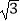
C.4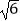
D.6 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知点A、B、C在同一直线上，M、N分别是AB，BC的中点．
(1)若AB=20，BC =8，求MN的长；
(2)若AB =a，BC =8，求MN的长；
(3)若AB =a，BC =b，求MN的长；
(4)从(1)(2)(3)的结果中能得到什么结论？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商场计划销售A，B两种型号的商品，经调查，用1500元采购A型商品的件数是用600元采购B型商品的件数的2倍，一件A型商品的进价比一件B型商品的进价多30元．
（1）求一件A，B型商品的进价分别为多少元？
（2）若该商场购进A，B型商品共100件进行试销，其中A型商品的件数不大于B型的件数，已知A型商品的售价为200元/件，B型商品的售价为180元/件，且全部能售出，求该商品能获得的利润最小是多少？
相关试题
