Question

【题目】直线与x轴交于点A，与y轴交于点B．点C是x轴上一动点，点D为（3，0），抛物线过B、C、D三点.

（1）如图1所示，若点C与点A关于y轴对称.

①求直线BD和抛物线的解析式；

②若点P是抛物线对称轴上一动点，当BP+CP的值最小时，求点P的坐标；

③若BD与抛物线的对称轴交于点M，点N在坐标轴上，以点N、B、D为顶点的三角形与△MCD相似，求所有满足条件的点N的坐标；

（2）如图2，若BE//x轴，且E（4，3），点A1与点A关于直线BC对称，当EA1的长最小时，直接写出OC的长.

Answer 1

【答案】（1）①y=x2﹣4x+3．②点P（2，1）．③（0，0），（﹣3，0）或（0，﹣3）．(2) OC=．

【解析】试题分析：（1）①由直线y=3x+3可得A、B点的坐标，再根据A、C关于y轴对称得到点C坐标，然后利用待定系数法即可得直线与抛物线的解析式；

②BD与对称轴的交点即为所求作的点；

③分情况讨论即可得；

（2）根据题意可知当点A1落在BE上时，EA1最小，由此即可得.

试题解析：（1）①∵直线l：y=3x+3与x轴交于点A，与y轴交于点B，

∴A（﹣1，0），B（0，3），

∵点A与点C关于y轴对称，

∴C（1，0），

设直线BD的解析式为：y=kx+b，

∵点B（0，3），D（3，0）在直线BD上，

∴ ，解得k=﹣1，b=3，

∴直线BD的解析式为：y=﹣x+3；

设抛物线的解析式为：y=a（x﹣1）（x﹣3），

∵点B（0，3）在抛物线上，

∴3=a×（﹣1）×（﹣3），

解得：a=1，

∴抛物线的解析式为：y=（x﹣1）（x﹣3）=x2﹣4x+3；

②点C关于对称轴的对称点为D，

直线BD的解析式为：y=﹣x+3，

当x=2时，y=1，

∴点P（2，1）；

③抛物线的解析式为：y=x2﹣4x+3=（x﹣2）2﹣1，

∴抛物线的对称轴为直线x=2，顶点坐标为（2，﹣1），

直线BD：y=﹣x+3与抛物线的对称轴交于点M，令x=2，得y=1，

∴M（2，1），

设对称轴与x轴交点为点F，则CF=FD=MF=1，

∴△MCD为等腰直角三角形，

∵以点N、B、D为顶点的三角形与△MCD相似，

∴△BND为等腰直角三角形，

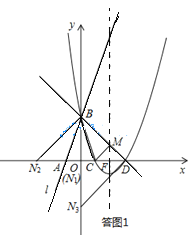
如答图1所示：

（I）若BD为斜边，则易知此时直角顶点为原点O，

∴N1（0，0）；

（II）若BD为直角边，B为直角顶点，则点N在x轴负半轴上，

∵OB=OD=ON2=3，

∴N2（﹣3，0）；

（III）若BD为直角边，D为直角顶点，则点N在y轴负半轴上，

∵OB=OD=ON3=3，

∴N3（0，﹣3），

∴满足条件的点N坐标为：（0，0），（﹣3，0）或（0，﹣3）；

（2）如图所示，当点A1在BE上是时，EA1最小，

由OB=3，OA=1，根据勾股定理可得AB= ，所以BA1=BA=，

易证明四边形ACA1B是菱形，所以AC=AB=，所以OC=-1.