【题目】如图1,已知线段AB两个端点坐标分别为A(a,0),B(0,b),且a,b满足:![]()
(1)填空:a= ,b= .

(2)在坐标轴上是否存在点C,使S△ABC=6,若存在,求出点C的坐标,符不存在,说明理由;
(3)如图2,若将线段Ba平移得到线段OD,其中B点对应O点,A点对应D点,点P(m,n)是线段OD上任意一点,请直接写出m与n的关系式。
参考答案:
【答案】(1) -6,4;(2) C坐标为(-9,0),(-3,0),(0,2),(0,6);(3)2m=3n(-6≤m≤0).
【解析】
(1)根据非负数的性质列方程求解即可;
(2)根据点B的坐标,求出B到x轴的距离,再利用三角形的面积求出AC的长度,然后分点C在A点的左边和右边两种情况讨论求解;
(3)根据平移求出点D的坐标,然后求出OD的解析式,再把P点的坐标代入求解即可.
解:(1)∵![]()
∴a=-6,b=4,
故答案为-6,4;
(2)由(1)知,a=-6,b=4,
∴A(-6,0),B(0,4),
当点C在x轴上时,设C(c,0),
∴AC=|c+6|,
∵S△ABC=6,![]()
∴c=-9或c=-3,
∴C(-9,0)或(-3,0),
当点C在y轴上时,设C(0,c'),
∴BC=|c'-4|,
∵S△ABC=6,![]()
∴c'=2或c'=6,
∴C(0,2)或(0,6),
即:满足条件的点C坐标为(-9,0),(-3,0),(0,2),(0,6);
(3)由(2)知,A(-6,0),B(0,4),
∵将线段BA平移得到线段OD,其中B点对应O点,A点对应D,
∴线段AB向下平移4个单位到线段OD,
∴D(-6,-4),设线段OD所在直线解析式为y=kx,
∴-6k=-4,
-
科目: 来源: 题型:
查看答案和解析>>【题目】设x是正实数,我们用{x}表示不小于x的最小正整数,如{0.7}=1,{2}=2,{3.1}=4,在此规定下任一正实数都能写成如下形式:x={x}-m,其中O≤m<l.
(1)直接写出{x}与x,x+1的大小关系:
(2)根据(1)中的关系式,求满足{2x-1}=3的x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若顺次连结四边形各边中点所得的四边形是矩形,则原四边形( )
A. 一定是矩形 B. 一定是菱形 C. 对角线一定相等 D. 对角线一定互相垂直
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:用3辆A型车和2辆B型车载满货物一次可运货17吨;用2辆A型车和3辆B型车载满货物一次可运货l8吨,某物流公刊现有35吨货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物.
根据以上信息,解答下列问题:
(1)l辆A型车和l辆B型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若A型车每辆需租金200元/次,B型车每辆需租金240元/次,请选出最省钱的租车方案,并求出最少租车费.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )

A. (
 ,0) B. (2,0) C. (
,0) B. (2,0) C. ( ,0) D. (3,0)
,0) D. (3,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织学生书法比赛,对参赛作品按A、B、C、D四个等级进行了评定.现随机抽取部分学生书法作品的评定结果进行分析,并绘制扇形统计图和条形统计图如下:
根据上述信息完成下列问题:
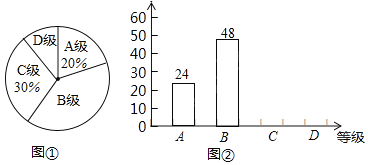
(1)在这次抽样调查中,共抽查了多少名学生?
(2)请在图②中把条形统计图补充完整;
(3)求出扇形统计图中“D级”部分所对应的扇形圆心角的大小;
(4)已知该校这次活动共收到参赛作品750份,请你估计参赛作品达到B级以上(即A级和B级)有多少份?
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:

⑴ 作出△
 绕点A逆时针旋转90°的△AB1C1,再作出△AB1C1关于原点O成中心对称的△A1B2C2.
绕点A逆时针旋转90°的△AB1C1,再作出△AB1C1关于原点O成中心对称的△A1B2C2.(2)请直接写出以A1、B2、C2为顶点的平行四边形的第四个顶点D的坐标 .(写出一个即可)
相关试题

