【题目】某校组织学生书法比赛,对参赛作品按A、B、C、D四个等级进行了评定.现随机抽取部分学生书法作品的评定结果进行分析,并绘制扇形统计图和条形统计图如下:
根据上述信息完成下列问题:
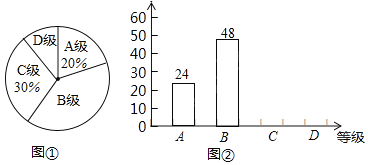
(1)在这次抽样调查中,共抽查了多少名学生?
(2)请在图②中把条形统计图补充完整;
(3)求出扇形统计图中“D级”部分所对应的扇形圆心角的大小;
(4)已知该校这次活动共收到参赛作品750份,请你估计参赛作品达到B级以上(即A级和B级)有多少份?
参考答案:
【答案】(1)这次抽取的学生数为120人;(2)补图见解析;(3)“D级”部分所对应的扇形圆心角为36°;(4)有450份.
【解析】分析:(1)根据A级人数为24人,以及在扇形图中所占比例为20%,24÷20%即可得出抽查了多少名学生;
(2)根据C级在扇形图中所占比例为30%,得出C级人数为:120×30%=36人,即可得出D级人数,补全条形图即可;
(3)求得“D级”部分所占的百分数,再乘360°即可求出答案;
(4)根据A级和B级作品在样本中所占比例为:(24+48)÷120×100%=60%,即可得出该校这次活动共收到参赛作品750份,参赛作品达到B级以上的份数.
详解:
(1)∵A级人数为24人,在扇形图中所占比例为20%,
∴这次抽取的学生数为:24÷20%=120人;
(2)根据C级在扇形图中所占比例为30%,得出C级人数为:120×30%=36人,
∴D级人数为:120﹣36﹣24﹣48=12人,
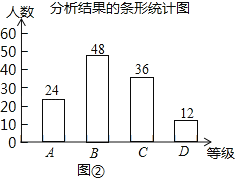
如图所示:
(3)360°×![]() =36°
=36°
答:“D级”部分所对应的扇形圆心角为36°;
(4)∵A级和B级作品在样本中所占比例为:(24+48)÷120×100%=60%,
∴该校这次活动共收到参赛作品750份,参赛作品达到B级以上有750×60%=450份.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:用3辆A型车和2辆B型车载满货物一次可运货17吨;用2辆A型车和3辆B型车载满货物一次可运货l8吨,某物流公刊现有35吨货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物.
根据以上信息,解答下列问题:
(1)l辆A型车和l辆B型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若A型车每辆需租金200元/次,B型车每辆需租金240元/次,请选出最省钱的租车方案,并求出最少租车费.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知线段AB两个端点坐标分别为A(a,0),B(0,b),且a,b满足:
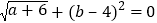
(1)填空:a= ,b= .

(2)在坐标轴上是否存在点C,使S△ABC=6,若存在,求出点C的坐标,符不存在,说明理由;
(3)如图2,若将线段Ba平移得到线段OD,其中B点对应O点,A点对应D点,点P(m,n)是线段OD上任意一点,请直接写出m与n的关系式。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )

A. (
 ,0) B. (2,0) C. (
,0) B. (2,0) C. ( ,0) D. (3,0)
,0) D. (3,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:

⑴ 作出△
 绕点A逆时针旋转90°的△AB1C1,再作出△AB1C1关于原点O成中心对称的△A1B2C2.
绕点A逆时针旋转90°的△AB1C1,再作出△AB1C1关于原点O成中心对称的△A1B2C2.(2)请直接写出以A1、B2、C2为顶点的平行四边形的第四个顶点D的坐标 .(写出一个即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的
 后得到线段CD,则点B的对应点D的坐标为( )
后得到线段CD,则点B的对应点D的坐标为( ) 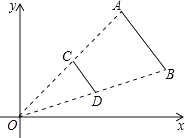
A.(3,3)
B.(1,4)
C.(3,1)
D.(4,1) -
科目: 来源: 题型:
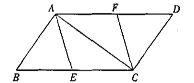
查看答案和解析>>【题目】如图,E、F分别是□ABCD的边BC、AD上的点,且BE=DF
(1)求证:四边形AECF是平行四边形;
(2)若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长.
相关试题

