【题目】如图是某地下商业街的入口,数学课外兴趣小组的同学打算运用所学的知识测量侧面支架的最高点E到地面的距离EF.经测量,支架的立柱BC与地面垂直,即∠BCA=90°,且BC=1.5m,点F、A、C在同一条水平线上,斜杆AB与水平线AC的夹角∠BAC=30°,支撑杆DE⊥AB于点D,该支架的边BE与AB的夹角∠EBD=60°,又测得AD=1m.请你求出该支架的边BE及顶端E到地面的距离EF的长度.
参考答案:
【答案】解:过B作BH⊥EF于点H,

∴四边形BCFH为矩形,BC=HF=1.5m,∠HBA=∠BAC=30°,
在Rt△ABC中,
∵∠BAC=30°,BC=1.5m,
∴AB=3m,
∵AD=1m,
∴BD=2m,
在Rt△EDB中,
∵∠EBD=60°,
∴∠BED=90°﹣60°=30°,
∴EB=2BD=2×2=4m,
又∵∠HBA=∠BAC=30°,
∴∠EBH=∠EBD﹣∠HBD=30°,
∴EH= ![]() EB=2m,
EB=2m,
∴EF=EH+HF=2+1.5=3.5(m).
答:该支架的边BE为4m,顶端E到地面的距离EF的长度为3.5m.
【解析】由直角三角形中30°所对的直角边等于斜边的一半可得由于∠BAC=30°,BC=1.5m,所以AB=3m,从而AD=1m,BD=2m。再利用性质直角三角形中30°所对的直角边等于斜边的一半容易算得EB=2BD=2×2=4m。
在计算顶端E到地面的距离EF的长度时,我们可以做辅助线把EF分为EH和HF两部分,其中HF等于BC等于1.5m,而EH仍然可用直角三角形中30°所对的直角边等于斜边的一半易得EH=![]() EB=2m,最后得到EF的长度为3.5m
EB=2m,最后得到EF的长度为3.5m
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2-4x-m2=0
(1)求证:该方程有两个不等的实根;
(2)若该方程的两实根x1、x2满足x1+2x2=9,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】合肥市某学校搬迁,教师和学生的寝室数量在增加,若该校今年准备建造三类不同的寝室,分别为单人间(供一个人住宿),双人间(供两个人住宿),四人间(供四个人住宿).因实际需要,单人间的数量在20至30之间(包括20和30),且四人间的数量是双人间的5倍.
(1)若2015年学校寝室数为64个,2017年建成后寝室数为121个,求2015至2017年的平均增长率;
(2)若建成后的寝室可供600人住宿,求单人间的数量;
(3)若该校今年建造三类不同的寝室的总数为180个,则该校的寝室建成后最多可供多少师生住宿?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正比例函数y=k1x的图象与反比例函数y=
 的图象的一个交点是(2,3).
的图象的一个交点是(2,3).
(1)求出这两个函数的表达式;
(2)作出两个函数的草图,利用你所作的图形,猜想并验证这两个函数图象的另一个交点的坐标;
(3)直接写出使反比例函数值大于正比例函数值的x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】对非负实数x“四舍五入”到个位的值记为(x).即当n为非负整数时,若n-
 ≤x<n+
≤x<n+ ,则(x)=n.如(0.46)=0,(3.67)=4.给出下列关于(x)的结论:①(1.493)=1;②(2x)=2(x);③若(
,则(x)=n.如(0.46)=0,(3.67)=4.给出下列关于(x)的结论:①(1.493)=1;②(2x)=2(x);③若( x-1)=4,则实数x的取值范围是9≤x<11;④当x≥0时,m为非负整数时,有(m+2017x)=m+(2017x);⑤(x+y)=(x)+(y).其中正确的结论有________________.(填序号)
x-1)=4,则实数x的取值范围是9≤x<11;④当x≥0时,m为非负整数时,有(m+2017x)=m+(2017x);⑤(x+y)=(x)+(y).其中正确的结论有________________.(填序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ACB中,∠C=90°,AC=30cm,BC=25cm,动点P从点C出发,沿CA方向运动,速度是2cm/s,动点Q从点B出发,沿BC方向运动,速度是1cm/s.

(1)几秒后P、Q两点相距25cm?
(2)几秒后△PCQ与△ABC相似?
(3)设△CPQ的面积为S1 , △ABC的面积为S2 , 在运动过程中是否存在某一时刻t,使得S1:S2=2:5?若存在,求出t的值;若不存在,则说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程中,有两个不相等实数根的是( )
A.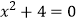
B.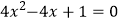
C.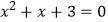
D.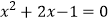
相关试题

