【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,
上,![]() ,连接
,连接![]() ,点
,点![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 的中点.
的中点.
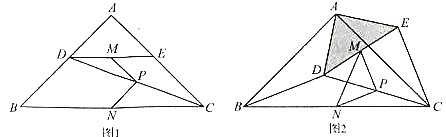
(1)观察猜想
图1中,线段![]() 与
与![]() 的数量关系是 ,位置关系是 ;
的数量关系是 ,位置关系是 ;
(2)探究证明
把![]() 绕点
绕点![]() 逆时针方向旋转到图2的位置,连接
逆时针方向旋转到图2的位置,连接![]() ,
,![]() ,
,![]() ,判断
,判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)拓展延伸
把![]() 绕点
绕点![]() 在平面内自由旋转,若
在平面内自由旋转,若![]() ,
,![]() ,请直接写出
,请直接写出![]() 面积的最大值.
面积的最大值.
参考答案:
【答案】(1)PM=PN,![]() ;(2)等腰直角三角形,理由详见解析;(3)
;(2)等腰直角三角形,理由详见解析;(3)![]() .
.
【解析】
试题分析:(1)已知 点![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 的中点,根据三角形的中位线定理可得
的中点,根据三角形的中位线定理可得![]() ,
,![]() ,
,![]() ,根据平行线的性质可得∠DPM=∠DCE,∠NPD=∠ADC,在
,根据平行线的性质可得∠DPM=∠DCE,∠NPD=∠ADC,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,可得BD=EC,∠DCE+∠ADC=90°,即可得PM=PN,∠DPM+∠NPD=90°,即
,可得BD=EC,∠DCE+∠ADC=90°,即可得PM=PN,∠DPM+∠NPD=90°,即![]() ;(2)
;(2)![]() 是等腰直角三角形,根据旋转的性质易证△BAD≌△CAE,即可得BD=CE,∠ABD=∠ACE,根据三角形的中位线定理及平行线的性质(方法可类比(1)的方法)可得PM=PN, ∠MPD=∠ECD,∠PNC=∠DBC,所以∠MPD=∠ECD=∠ACD+∠ACE=∠ACD+∠ABD,∠DPN=∠PNC+∠PCN =∠DBC+∠PCN,即可得∠MPN=∠MPD+∠DPN=∠ACD+∠ABD+∠DBC+∠PCN=∠ABC+∠ACB=90°,即△PMN为等腰直角三角形;(3)把
是等腰直角三角形,根据旋转的性质易证△BAD≌△CAE,即可得BD=CE,∠ABD=∠ACE,根据三角形的中位线定理及平行线的性质(方法可类比(1)的方法)可得PM=PN, ∠MPD=∠ECD,∠PNC=∠DBC,所以∠MPD=∠ECD=∠ACD+∠ACE=∠ACD+∠ABD,∠DPN=∠PNC+∠PCN =∠DBC+∠PCN,即可得∠MPN=∠MPD+∠DPN=∠ACD+∠ABD+∠DBC+∠PCN=∠ABC+∠ACB=90°,即△PMN为等腰直角三角形;(3)把![]() 绕点
绕点![]() 旋转到如图的位置,此时PN=
旋转到如图的位置,此时PN=![]() (AD+AB)=7, PM=
(AD+AB)=7, PM=![]() (AE+AC)=7,且PN、PM的值最长,由(2)可知PM=PN,
(AE+AC)=7,且PN、PM的值最长,由(2)可知PM=PN,![]() ,所以
,所以![]() 面积的最大值为
面积的最大值为![]() .
.

试题解析:
(1)PM=PN,![]() ;
;
(2)等腰直角三角形,理由如下:
由旋转可得∠BAD=∠CAE,
又AB=AC,AD=AE
∴△BAD≌△CAE
∴BD=CE,∠ABD=∠ACE,
∵点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点
的中点
∴PM是△DCE的中位线
∴PM=![]() CE,且
CE,且![]() ,
,
同理可证PN=![]() BD,且
BD,且![]()
∴PM=PN, ∠MPD=∠ECD,∠PNC=∠DBC,
∴∠MPD=∠ECD=∠ACD+∠ACE=∠ACD+∠ABD,
∠DPN=∠PNC+∠PCN =∠DBC+∠PCN,
∴∠MPN=∠MPD+∠DPN=∠ACD+∠ABD+∠DBC+∠PCN=∠ABC+∠ACB=90°,
即△PMN为等腰直角三角形.
(3)![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角梯形ABCD中,AD∥BC,AB=
 cm,AD=24cm,BC=26cm,∠B=90°,动点P从A开始沿AD边向D以1cm/s的速度运动,动点Q从点C开始沿CB以3cm/s的速度向点B运动.P、Q同时出发,当其中一点到达顶点时,另一点也随之停止运动,设运动时间为ts,问:
cm,AD=24cm,BC=26cm,∠B=90°,动点P从A开始沿AD边向D以1cm/s的速度运动,动点Q从点C开始沿CB以3cm/s的速度向点B运动.P、Q同时出发,当其中一点到达顶点时,另一点也随之停止运动,设运动时间为ts,问: 
(1)t=时,四边形PQCD是平行四边形.
(2)是否存在一个t值,使PQ把梯形ABCD分成面积相等的两部分?若存在请求出t的值.
(3)当t为何值时,四边形PQCD为等腰梯形.
(4)连接DQ,是否存在t值使△CDQ为等腰三角形?若存在请直接写出t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人在跳远练习中,6次成绩分别为(单位:米): 甲:3.8 3.8 3.9 3.9 4.0 4.0; 乙:3.8 3.9 3.9 3.9 3.9 4.0.
则这次跳远练习中,甲乙两人成绩方差的大小关系是( )
A. >
> 
B. <
< 
C. =
= 
D.无法确定 -
科目: 来源: 题型:
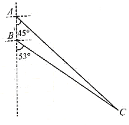
查看答案和解析>>【题目】如图所示,我国两艘海监船
 ,
, 在南海海域巡航,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船
在南海海域巡航,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船 .此时,
.此时,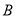 船在
船在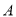 船的正南方向5海里处,
船的正南方向5海里处,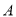 船测得渔船
船测得渔船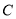 在其南偏东
在其南偏东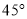 方向,
方向, 船测得渔船
船测得渔船 在其南偏东
在其南偏东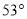 方向.已知
方向.已知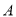 船的航速为30海里/小时,
船的航速为30海里/小时,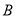 船的航速为25海里/小时,问
船的航速为25海里/小时,问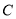 船至少要等待多长时间才能得到救援?(参考数据:
船至少要等待多长时间才能得到救援?(参考数据: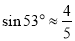 ,
,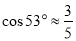 ,
,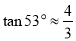 ,
,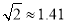 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】“中国天眼”500米口径球面射电望远镜的反射总面积约25万平方米,是世界射电望远镜之最,其中25万用科学记数法表示为( )
A.25×105B.0.25×106C.2.5×105D.2.5×106
-
科目: 来源: 题型:
查看答案和解析>>【题目】李老师骑自行车上班,最初以某一速度匀速行进,中途由于自行车故障,停下修车耽误了几分钟,为了按时到校,李老师加快了速度,仍保持匀速行进,结果准时到校.在课堂上,李老师请学生画出自行车行进路程y千米与行进时间t的函数图象的示意图,同学们画出的示意图如下,你认为正确的是( )
A.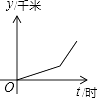
B.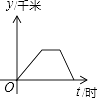
C.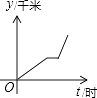
D.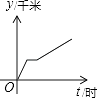
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个数的立方根是它本身,那么这个数是( )
A. 1、0 B. - 1 C. 0 D. 1 、 - 1、 0
相关试题

