【题目】如图,在半径为 ![]() 的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=4,则OP的长为( )
的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=4,则OP的长为( )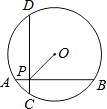
A.1
B.![]()
C.2
D.2 ![]()
参考答案:
【答案】B
【解析】解:作OE⊥AB于E,OF⊥CD于F,连结OD、OB,如图, 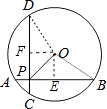
则AE=BE= ![]() AB=2,DF=CF=
AB=2,DF=CF= ![]() CD=2,
CD=2,
在Rt△OBE中,∵OB= ![]() ,BE=2,
,BE=2,
∴OE= ![]() =1,
=1,
同理可得OF=1,
∵AB⊥CD,
∴四边形OEPF为矩形,
而OE=OF=1,
∴四边形OEPF为正方形,
∴OP= ![]() OE=
OE= ![]() .
.
所以答案是:B.
【考点精析】关于本题考查的勾股定理的概念和垂径定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,已知点A(6,0),又点B(x,y)在第一象限内,且x+y=8,设△AOB的面积是S.
(1)写出S与x之间的函数解析式,并求出x的取值范围;
(2)画出(1)中所求函数的图象.

-
科目: 来源: 题型:
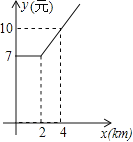
查看答案和解析>>【题目】某地出租车计费方法如图,x(km)表示行驶里程,y(元)表示车费,请根据图象解答下列问题:
(1)该地出租车的起步价是 元;
(2)当x>2时,求y与x之间的函数关系式;
(3)若某乘客有一次乘出租车的里程为18km,则这位乘客需付出租车车费多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知O为直线AB上的一点,∠COE是直角,OF平分∠AOE.
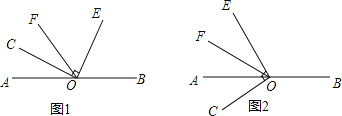
(1)如图1,若∠COF=34°,则∠BOE=______;
(2)如图1,若∠BOE=80°,则∠COF=______;
(3)若∠COF=m°,则∠BOE=______度;∠BOE与∠COF的数量关系为______.
(4)当∠COE绕点O逆时针旋转到如图2的位置时,(3)中∠BOE与∠COF的数量关系是否仍然成立?请说明理由.
-
科目: 来源: 题型:
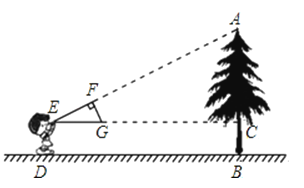
查看答案和解析>>【题目】如图,小明同学用自制的直角三角形纸板EFG测量树的高度AB,他调整自己的位置,设法使斜边EG保持水平,并且边EF所在的直线经过点A.已知纸板的两条直角边EF=60cm,FG=30cm,测得小刚与树的水平距离BD=8m,边EG离地面的高度DE=1.6m,则树的高度AB等于( )
A.5m
B.5.5m
C.5.6m
D.5.8m -
科目: 来源: 题型:
查看答案和解析>>【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城市街道上行驶速度不得超过70 km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30 m处,过了2 s后,测得小汽车与车速检测仪间距离为50 m,这辆小汽车超速了吗?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数学兴趣小组想测量电线杆AB的高度,他们发现电线杆的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4米,BC=10米,CD与地面成30°角,且此时测得1米杆的影长为2米,则电线杆的高度约为米(结果保留根号)

相关试题

