【题目】已知△ABC,O 是△ABC 所在平面内的一点,连接 OB、OC,将∠ABO、∠ACO分别记为∠1、∠2.
(1)如图(1),当点 O 在图中所示的位置时,∠1+∠2+∠A+∠O= ;
(2)如图(2),当点 O 在△ABC 的内部时,∠1、∠2、∠A、∠OC四个角之间满足怎样 的数量关系?请写出你的结论并说明理由;
(3)当点 O 在△ABC 所在平面内运动时(点 O 不在三边所在的直线上),由于所处的位 置不同,∠1、∠2、∠A、∠OC四个角之间满足的数量关系还存在着与(1)、(2) 中不同的结论,请在图(3)中画出一种不同的示意图,并直接写出相应的结论.

参考答案:
【答案】(1)360°;(2)∠O=∠1+∠2+∠A;(3)∠A=∠2+∠O-∠1;
【解析】
(1)根据四边形内角和定理解答即可;
(2)连接OA,并延长交BC于D点,根据三角形内角与外角的性质解答即可;
(3)根据题意画出图形,再写出结论.
 (1)如图(1),当点O与点A在直线BC的异侧时,
(1)如图(1),当点O与点A在直线BC的异侧时,
∵AB、OB、OC、AC四条线段正好构成四边形,
∴∠1+∠2+∠A+∠O=360;
(2)连接OA,并延长交BC于D点,
∵∠BOD是△AOB的外角,
∴∠OAB+∠1=∠BOD,
∵∠COD是△AOB的外角,
∴∠OAC+∠2=∠COD,
∴∠OAB+∠1+∠OAC+∠2=∠COD+∠BOD,
即∠1+∠2+∠A=∠O.
(3)如图所示,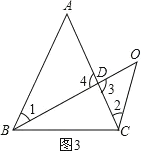
∠A=∠2+∠O∠1.
在△ABD中,∠4=180∠A∠1,
∵∠3=∠4,
∴∠3=180∠A∠1,
∴∠3+∠2+∠O=180,
∴180∠A∠1+∠2+∠O=180,
整理得,∠A=∠2+∠O∠1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABC1D1的边长为1,延长C1D1到A1,以A1C1为边向右作正方形A1C1C2D2,延长C2D2到A2,以A2C2为边向右作正方形A2C2C3D3(如图所示),以此类推…,若A1C1=2,且点A,D2, D3,…,D10都在同一直线上,则正方形A9C9C10D10的边长是______
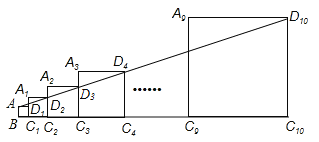
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将□ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
⑴求证:△ABF≌△ECF;⑵若∠AFC=2∠D,连接AC、BE.求证:四边形ABEC是矩形.
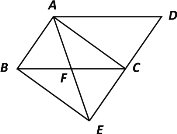
-
科目: 来源: 题型:
查看答案和解析>>【题目】一块木板如图所示,已知AB=4,BC=3,DC=12,AD=13,∠B=90°,木板的面积为( )

A. 60 B. 30 C. 24 D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB.添加一个条件,不能使四边形DBCE成为矩形的是( )

(A)AB=BE (B)BE⊥DC (C)∠ADB=90° (D)CE⊥DE
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a>b,则下列各式中正确的是( )
A. a-c<b-cB. ac>bcC. -
 (c≠0)D. a(c2+1)>b(c2+1)
(c≠0)D. a(c2+1)>b(c2+1) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,CD是边AB上的高,且
 .
.(1)求证:△ACD∽△CBD;
(2)求∠ACB的大小.

相关试题

