【题目】如图,已知A,O,B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC.
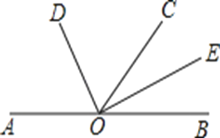
(1)若∠BOC=62°,求∠DOE的度数;
(2)若∠BOC=α,求∠DOE的度数;
(3)通过(1)(2)的计算,你能总结出什么结论,直接简写出来,不用说明理由.
参考答案:
【答案】(1)90°;(2)90°;(3)∠DOE=90°.
【解析】
(1)OD平分∠AOC,OE平分∠BOC,得出∠DOE![]() (∠BOC+∠COA),代入数据求得问题;
(∠BOC+∠COA),代入数据求得问题;
(2)利用(1)的结论,把∠BOC=a°,代入数据求得问题;
(3)根据(1)(2)即可得出结论.
(1)∵OD平分∠AOC,OE平分∠BOC,∴∠DOC![]() ∠AOC,∠COE
∠AOC,∠COE![]() ∠BOC,∴∠DOE=∠DOC+∠COE
∠BOC,∴∠DOE=∠DOC+∠COE![]() (∠BOC+∠COA)
(∠BOC+∠COA)![]() (62°+180°﹣62°)=90°;
(62°+180°﹣62°)=90°;
(2)∠DOE═![]() (∠BOC+∠COA)
(∠BOC+∠COA)![]() (a°+180°﹣a°)=90°;
(a°+180°﹣a°)=90°;
(3)由(1)(2)可得:∠DOE=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图A在数轴上对应的数为-2.
(1)点B在点A右边距离A点4个单位长度,则点B所对应的数是_____.
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点B以每秒3个单位长度沿数轴向右运动.现两点同时运动,当点A运动到-6的点处时,求A、B两点间的距离.
(3)在(2)的条件下,现A点静止不动,B点以原速沿数轴向左运动,经过多长时间A、B两点相距4个单位长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)(x-5)2=16 (直接开平方法) (2)x2+5x=0 (因式分解法)
(3)x2-4x+1=0 (配方法) (4)x2+3x-4=0 (公式法)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,一块Rt△ABC的绿地,量得两直角边AC=8cm,BC=6cm.现在要将这块绿地扩充成等腰△ABD,且扩充部分(△ADC)是以8cm为直角边长的直角三角形,求扩充等腰△ABD的周长.
(1)在图1中,当AB=AD=10cm时,△ABD的周长为 .
(2)在图2中,当BA=BD=10cm时,△ABD的周长为 .
(3)在图3中,当DA=DB时,求△ABD的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】
 操作思考:如图1,在平面直角坐标系中,等腰
操作思考:如图1,在平面直角坐标系中,等腰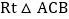 的直角顶点C在原点,将其绕着点O旋转,若顶点A恰好落在点
的直角顶点C在原点,将其绕着点O旋转,若顶点A恰好落在点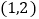 处
处 则
则 的长为______;
的长为______; 点B的坐标为______
点B的坐标为______ 直接写结果
直接写结果
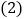 感悟应用:如图2,在平面直角坐标系中,将等腰
感悟应用:如图2,在平面直角坐标系中,将等腰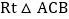 如图放置,直角顶点
如图放置,直角顶点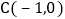 ,点
,点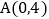 ,试求直线AB的函数表达式.
,试求直线AB的函数表达式.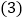 拓展研究:如图3,在直角坐标系中,点
拓展研究:如图3,在直角坐标系中,点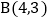 ,过点B作
,过点B作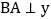 轴,垂足为点A,作
轴,垂足为点A,作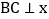 轴,垂足为点C,P是线段BC上的一个动点,点Q是直线
轴,垂足为点C,P是线段BC上的一个动点,点Q是直线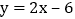 上一动点
上一动点 问是否存在以点P为直角顶点的等腰
问是否存在以点P为直角顶点的等腰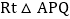 ,若存在,请求出此时P的坐标,若不存在,请说明理由.
,若存在,请求出此时P的坐标,若不存在,请说明理由.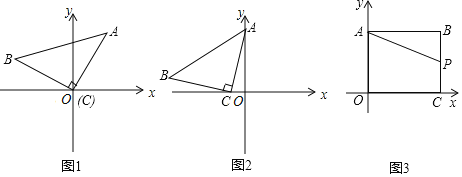
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
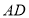 是
是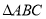 的边
的边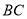 上的中线.
上的中线.(1)①用尺规完成作图:延长
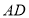 到点
到点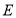 ,使
,使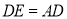 ,连接
,连接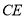 ;
;② 若
 ,求
,求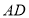 的取值范围;
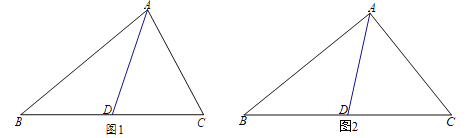
的取值范围;(2)如图2,当
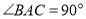 时,求证:
时,求证: .
.
-
科目: 来源: 题型:
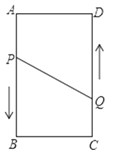
查看答案和解析>>【题目】如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2 cm/s的速度向D移动.
(1)P、Q两点从出发开始到几秒?四边形PBCQ的面积为33cm2;
(2)P、Q两点从出发开始到几秒时?点P和点Q的距离是10cm.
相关试题

