【题目】如图 (1),已知△ABC是等边三角形,以BC为直径的⊙O交AB、AC于D、E.求证:
(1)△DOE是等边三角形.
(2)如图(2),若∠A=60°,AB≠AC , 则(1)中结论是否成立?如果成立,请给出证明;如果不成立,请说明理由.
参考答案:
【答案】
(1)
证明:∵△ABC为等边三角形,
∴∠B=∠C=60°.
∵OB=OC=OE=OD,∴△OBD和△OEC都为等边三角形.
∴∠BOD=∠EOC=60°.∴∠DOE=60°.
∴△DOE为等边三角形.
(2)
解:当∠A=60°,AB≠AC时,(1)中的结论仍然成立.
证明:连结CD.∵BC为⊙O的直径,
∴∠BDC=90°.∴∠ADC=90°.
∵∠A=60°,∴∠ACD=30°.∴∠DOE=2∠ACD=60°.
∵OD=OE,∴△DOE为等边三角形.
【解析】(1)证明:∵△ABC为等边三角形,
∴∠B=∠C=60°.
∵OB=OC=OE=OD,∴△OBD和△OEC都为等边三角形.
∴∠BOD=∠EOC=60°.∴∠DOE=60°.
∴△DOE为等边三角形.
(2)当∠A=60°,AB≠AC时,(1)中的结论仍然成立.
证明:连结CD.∵BC为⊙O的直径,
∴∠BDC=90°.∴∠ADC=90°.
∵∠A=60°,∴∠ACD=30°.∴∠DOE=2∠ACD=60°.
∵OD=OE,∴△DOE为等边三角形.
【考点精析】本题主要考查了等边三角形的性质和圆周角定理的相关知识点,需要掌握等边三角形的三个角都相等并且每个角都是60°;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上点A表示数a,点B表示数b,点C表示数c,b是最小的正整数,且a,c满足|a+2|+(c-7)2=0.
(1)填空:a=________,b=________,c=________;
(2)画出数轴,并把A,B,C三点表示在数轴上;
(3)P是数轴上任意一点,点P表示的数是x,当PA+PB+PC=10时,x的值为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y是x的反比例函数,且当x=-4时,y=
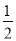 ,
,(1)求这个反比例函数关系式和自变量x的取值范围;
(2)求当x=6时函数y的值.
【答案】(1)
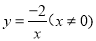 (2)
(2)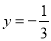
【解析】整体分析:
(1)由反比例函数的这定义求k值,确定x的取值范围;(2)把x=6代入(1)中求得的反比例函数的解析式.
解:(1)设反比例函数关系式为
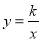 ,
,则k=-4×
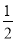 =-2,
=-2,所以个反比例函数关系式是
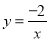 ,自变量x的取值范围是x≠0.
,自变量x的取值范围是x≠0.(2)当x=6时,
 =
=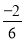 =-
=-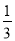 .
.【题型】解答题
【结束】
18【题目】如图,函数y=
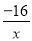 和y= - x+4的图像交点为A、B,原点为O,求△AOB面积.
和y= - x+4的图像交点为A、B,原点为O,求△AOB面积.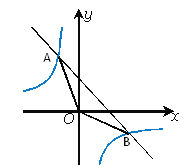
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个3×3的方格中填写了9个数字,使得每行、每列、每条对角线上的三个数之和相等,得到的3×3的方格称为一个三阶幻方.
(1)在图1中空格处填上合适的数字,使它构成一个三阶幻方;
(2)如图2的方格中填写了一些数和字母,当x+y的值为多少时,它能构成一个三阶幻方.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,函数y=
 和y= - x+4的图像交点为A、B,原点为O,求△AOB面积.
和y= - x+4的图像交点为A、B,原点为O,求△AOB面积.
【答案】8

【解析】整体分析:
联立方程y=
 和y= - x+4,求出点A,B的坐标,然后由公式△OAB的面积=
和y= - x+4,求出点A,B的坐标,然后由公式△OAB的面积= ×(x1- x2)(y2- y1)求解.
×(x1- x2)(y2- y1)求解.解:把y=
 代入y= - x+4得,
代入y= - x+4得, = - x+4,
= - x+4,解得x1=2+
 ,x2=2-
,x2=2- .
.所以y1=2-
 ,y2=2+
,y2=2+ .
.则A(2-
 ,2+
,2+ ),B(2+
),B(2+ ,2-
,2- ),
),所以△OAB的面积=
 ×(x1- x2)(y2- y1)==
×(x1- x2)(y2- y1)== ×4
×4 ×4
×4 =
= .
.【题型】解答题
【结束】
19【题目】如图,直线
 与双曲线
与双曲线 相交于A(2,1)、B两点.
相交于A(2,1)、B两点.
(1)求m及k的值;
(2)不解关于x、y的方程组
 直接写出点B的坐标;
直接写出点B的坐标;(3)直线
 经过点B吗?请说明理由.
经过点B吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
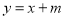 与双曲线
与双曲线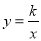 相交于A(2,1)、B两点.
相交于A(2,1)、B两点.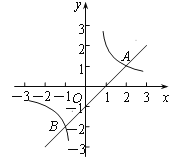
(1)求m及k的值;
(2)不解关于x、y的方程组
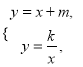 直接写出点B的坐标;
直接写出点B的坐标;(3)直线
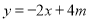 经过点B吗?请说明理由.
经过点B吗?请说明理由.【答案】(1)m=-1,k=2;(2)(-1,-2);(3)经过
【解析】试题分析:(1)把A(2,1)分别代入直线
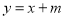 与双曲线
与双曲线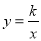 即可求得结果;
即可求得结果;(2)根据函数图象的特征写出两个图象的交点坐标即可;
(3)把x=-1,m=-1代入
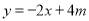 即可求得y的值,从而作出判断.
即可求得y的值,从而作出判断.(1)把A(2,1)分别代入直线
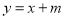 与双曲线
与双曲线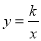 的解析式得m=-1,k=2;
的解析式得m=-1,k=2;(2)由题意得B的坐标(-1,-2);
(3)当x=-1,m=-1代入
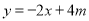 得y=-2×(-1)+4×(-1)=2-4=-2
得y=-2×(-1)+4×(-1)=2-4=-2所以直线
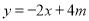 经过点B(-1,-2).
经过点B(-1,-2).考点:反比例函数的性质
点评:反比例函数的性质是初中数学的重点,是中考常见题,一般难度不大,需熟练掌握.
【题型】解答题
【结束】
20【题目】某气球内充满了一定质量的气球,当温度不变时,气球内气球的压力p(千帕)是气球的体积V(米2)的反比例函数,其图象如图所示(千帕是一种压强单位)
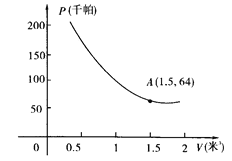
(1)写出这个函数的解析式;
(2)当气球的体积为0.8立方米时,气球内的气压是多少千帕;
(3)当气球内的气压大于144千帕时,气球将爆炸,为了安全起见,气球的体积应不小于多少立方米。
相关试题

