【题目】如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB于点E.若PE=2,则两平行线AD与BC间的距离为( ) 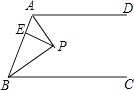
A.4
B.5
C.6
D.7
参考答案:
【答案】A
【解析】解:过点P作MN⊥AD, ∵AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,PE⊥AB于点E,
∴AP⊥BP,PN⊥BC,
∴PM=PE=2,PE=PN=2,
∴MN=2+2=4;
故选A.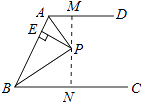
【考点精析】关于本题考查的平行线之间的距离和角平分线的性质定理,需要了解两条平行线的距离:两条直线平行,从一条直线上的任意一点向另一条直线引垂线,垂线段的长度,叫做两条平行线的距离;定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元
(1) 求甲、乙两种商品每件的进价分别是多少元?
(2) 商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式(组),并把它们的解集在数轴上表示出来.
(1)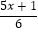 ﹣2>
﹣2> 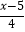

(2)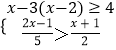 .
. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. ﹣1﹣1=0 B. ﹣1+1=0
C. 1﹣(﹣1)=0 D. (﹣1)+(﹣1)=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题10分)对于平面直角坐标系xOy中的点P(a,b),若点P的坐标为(a+
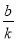 ,ka+b)(k为常数,k≠0),则称点P′为点P的“k属派生点”.例如:P(1,4)的“2属派生点”为P′(1+
,ka+b)(k为常数,k≠0),则称点P′为点P的“k属派生点”.例如:P(1,4)的“2属派生点”为P′(1+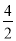 ,2×1+4),即P′(3,6).
,2×1+4),即P′(3,6).(1) ① 点P(-1,-2)的“2属派生点”P′的坐标为_______________
② 若点P的“k属派生点”为P′(3,3),请写出一个符合条件的点P的坐标_____________
(2) 若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且△OPP′为等腰直角三角形,则k的值为____________
(3) 如图,点Q的坐标为(0,
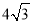 ),点A在函数
),点A在函数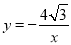 (x<0)的图象上,且点A是点B的“
(x<0)的图象上,且点A是点B的“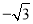 属派生点”.当线段BQ最短时,求B点坐标.
属派生点”.当线段BQ最短时,求B点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程3x=12的解有___个,不等式3x<12的解有____个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】6.8×105这个数的原数是( )
A. 68000B. 680000C. 0.000086D. ﹣680000
相关试题

