【题目】解不等式(组),并把它们的解集在数轴上表示出来.
(1)![]() ﹣2>
﹣2> ![]()
![]()
(2)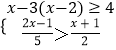 .
. ![]()
参考答案:
【答案】
(1)
解:去分母,得:2(5x+1)﹣24>3(x﹣5),
去括号,得:10x+2﹣24>3x﹣15,
移项,得:10x﹣3x>﹣15﹣2+24,
合并同类项,得:7x>7,
系数化为1,得:x>1;
将解集表示在数轴上如下:

(2)
解:解不等式x﹣3(x﹣2)≥4,得:x≤1,
解不等式 ![]() >
> ![]() ,得:x<﹣7,
,得:x<﹣7,
∴不等式组的解集为:x<﹣7,
将解集表示在数轴上如下:
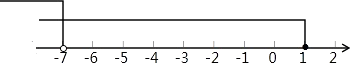
【解析】(1)根据解一元一次不等式基本步骤:去分母、去括号、移项、合并同类项、系数化为1可得;(2)分别求出每一个不等式的解集,根据口诀:“同小取小”确定不等式组的解集.
【考点精析】关于本题考查的不等式的解集在数轴上的表示和一元一次不等式的解法,需要了解不等式的解集可以在数轴上表示,分三步进行:①画数轴②定界点③定方向.规律:用数轴表示不等式的解集,应记住下面的规律:大于向右画,小于向左画,等于用实心圆点,不等于用空心圆圈;步骤:①去分母;②去括号;③移项;④合并同类项; ⑤系数化为1(特别要注意不等号方向改变的问题)才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校体育组对本校九年级全体同学体育测试情况进行调查,他们随即抽查部分同学体育测试成绩(由高到低分四个等级),根据调查的数据绘制成如下的条形统计图和扇形统计图:
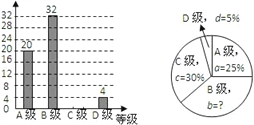
请根据以上不完整的统计图提供的信息,解答下列问题:
(1) 该课题研究小组共抽查了_________名同学的体育测试成绩,扇形统计图中B级所占的百分比b=__________
(2) 补全条形统计图.
(3) 若该校九年级共有200名同学,请估计该校九年级同学体育测试达标(测试成绩C级以上,含C级)均有___________名.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(x+2)(3x﹣5)=3x2﹣bx﹣10,则b= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元
(1) 求甲、乙两种商品每件的进价分别是多少元?
(2) 商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. ﹣1﹣1=0 B. ﹣1+1=0
C. 1﹣(﹣1)=0 D. (﹣1)+(﹣1)=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB于点E.若PE=2,则两平行线AD与BC间的距离为( )
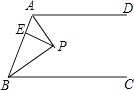
A.4
B.5
C.6
D.7 -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题10分)对于平面直角坐标系xOy中的点P(a,b),若点P的坐标为(a+
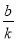 ,ka+b)(k为常数,k≠0),则称点P′为点P的“k属派生点”.例如:P(1,4)的“2属派生点”为P′(1+
,ka+b)(k为常数,k≠0),则称点P′为点P的“k属派生点”.例如:P(1,4)的“2属派生点”为P′(1+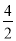 ,2×1+4),即P′(3,6).
,2×1+4),即P′(3,6).(1) ① 点P(-1,-2)的“2属派生点”P′的坐标为_______________
② 若点P的“k属派生点”为P′(3,3),请写出一个符合条件的点P的坐标_____________
(2) 若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且△OPP′为等腰直角三角形,则k的值为____________
(3) 如图,点Q的坐标为(0,
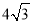 ),点A在函数
),点A在函数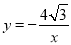 (x<0)的图象上,且点A是点B的“
(x<0)的图象上,且点A是点B的“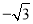 属派生点”.当线段BQ最短时,求B点坐标.
属派生点”.当线段BQ最短时,求B点坐标.
相关试题

