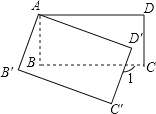
【题目】如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=110°,则∠α= .
参考答案:
【答案】![]() 。
。
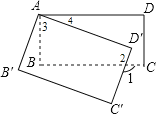
【解析】试题分析:根据矩形的性质得∠B=∠D=∠BAD=90°,根据旋转的性质得∠D′=∠D=90°,∠4=α,利用对顶角相等得到∠1=∠2=110°,再根据四边形的内角和为360°可计算出∠3=70°,然后利用互余即可得到∠α的度数.
解:如图,
∵四边形ABCD为矩形,
∴∠B=∠D=∠BAD=90°,
∵矩形ABCD绕点A顺时针旋转得到矩形AB′C′D′,
∴∠D′=∠D=90°,∠4=α,
∵∠1=∠2=110°,
∴∠3=360°﹣90°﹣90°﹣110°=70°,
∴∠4=90°﹣70°=20°,
∴∠α=20°.
故答案为:20°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2-(2k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB,AC的长是这个方程的两个实数根,第三边BC的长为5,当△ABC是等腰三角形时,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某旅行社的一则广告如下:我社推出去井冈山红色旅游,收费标准为:如果组团人数不超过30人,人均收费800元;如果人数多于30人,那么每增加1人,人均收费降低10元,但人均收费不得低于500元,甲公司想分批组织员工到井冈山红色旅游学习.
(1)如果第一批组织38人去学习,则公司应向旅行社交费 元;
(2)如果公司计划用29250元组织第一批员工去学习,问这次旅游学习应安排多少人参加?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
(1)求证:CD为⊙O的切线;
(2)若BD的弦心距OF=1,∠ABD=30°,求图中阴影部分的面积.(结果保留π)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示:在平面直角坐标系中,四边形OACB为矩形,C点坐标为(3,6),若点P从O点沿OA向A点以1cm/s的速度运动,点Q从A点沿AC以2cm/s的速度运动,如果P、Q分别从O、A同时出发,问:
(1)经过多长时间△PAQ的面积为2cm
 ?
?(2)△PAQ的面积能否达到3 cm
 ?
?(3)经过多长时间,P、Q两点之间的距离为
 cm?
cm?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的正方形网格中,△ABC 的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
(1)以A点为旋转中心,将△ABC绕点A顺时针旋转90°得△AB1C1,画出△AB1C1.
(2)作出△ABC关于坐标原点O成中心对称的△A2B2C2.
(3)作出点C关于x轴的对称点P. 若点P向右平移x个单位长度后落在△A2B2C2的内部(不含落在△A2B2C2的边上),请直接写出x的取值范围..
(提醒:每个小正方形边长为1个单位长度)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半圆O的直径MN=6cm,在△ABC中,∠ACB=90°,∠ABC=30°,BC=6cm,半圆O以1cm/s的速度从左向右运动,在运动过程中,点M、N始终在直线BC上,设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=4cm.

(1)当t为何值时,△ABC的一边所在的直线与半圆O所在的圆相切?
(2)当△ABC的一边所在的直线与半圆O所在圆相切时,如果半圆O与直线MN围成的区域与△ABC三边围成的区域有重叠部分,求重叠部分的面积.
相关试题

