【题目】某旅行社的一则广告如下:我社推出去井冈山红色旅游,收费标准为:如果组团人数不超过30人,人均收费800元;如果人数多于30人,那么每增加1人,人均收费降低10元,但人均收费不得低于500元,甲公司想分批组织员工到井冈山红色旅游学习.
(1)如果第一批组织38人去学习,则公司应向旅行社交费 元;
(2)如果公司计划用29250元组织第一批员工去学习,问这次旅游学习应安排多少人参加?
参考答案:
【答案】(1)27360;(2)应安排45人参加
【解析】试题分析:
(1)由题意可列出式子:38×[800﹣(38﹣30)×10]计算可得结果;
(2)首先由30×800=24000<29250,可知这次去旅游的人数超过了30人,
设安排了![]() 人去旅游,由题意可列方程:
人去旅游,由题意可列方程: ![]() ,解方程求得
,解方程求得![]() 的值后,再由人均费用不低于500元进行检验即可得到答案.
的值后,再由人均费用不低于500元进行检验即可得到答案.
试题解析:
(1)∵人数多于30人,那么每增加1人,人均收费降低10元,
∴第一批组织38人去学习,则公司应向旅行社交费:38×[800﹣(38﹣30)×10]=27360;
故答案为:27360;
(2)设这次旅游安排了![]() 人参加,
人参加,
∵30×800=24000<29250,
∴![]() >30,根据题意得:
>30,根据题意得:
![]() ,
,
整理得, ![]() ,
,
解得: ![]() ,
,
∵800﹣10(![]() ﹣30)≥500,
﹣30)≥500,
∴![]() ≤60,
≤60,
∴![]() =45.
=45.
答:这次旅游应安排45人参加.
-
科目: 来源: 题型:
查看答案和解析>>【题目】市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次
第二次
第三次
第四次
第五次
第六次
甲
10
8
9
8
10
9
乙
10
7
10
10
9
8
(1)根据表格中的数据,分别计算甲、乙的平均成绩;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加省比赛更合适,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半圆O的直径MN=6cm,在△ABC中,∠ACB=90°,∠ABC=30°,BC=6cm,半圆O以1cm/s的速度从左向右运动,在运动过程中,点M、N始终在直线BC上,设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=4cm.

(1)当t为何值时,△ABC的一边所在的直线与半圆O所在的圆相切?
(2)当△ABC的一边所在的直线与半圆O所在圆相切时,如果半圆O与直线MN围成的区域与△ABC三边围成的区域有重叠部分,求重叠部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列从左到右的变形,是分解因式的是( )
A. xy2(x-1)=x2y2-xy2 B. x2+x-5=(x-2)(x+3)+1
C. (a+3)(a-3)=a2-9 D. 2a2+4a=2a(a+2)
-
科目: 来源: 题型:
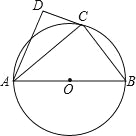
查看答案和解析>>【题目】如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.
(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2-(2k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB,AC的长是这个方程的两个实数根,第三边BC的长为5,当△ABC是等腰三角形时,求k的值.
-
科目: 来源: 题型:
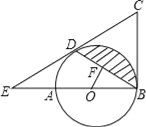
查看答案和解析>>【题目】如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
(1)求证:CD为⊙O的切线;
(2)若BD的弦心距OF=1,∠ABD=30°,求图中阴影部分的面积.(结果保留π)
相关试题

