【题目】如图,半圆O的直径MN=6cm,在△ABC中,∠ACB=90°,∠ABC=30°,BC=6cm,半圆O以1cm/s的速度从左向右运动,在运动过程中,点M、N始终在直线BC上,设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=4cm.

(1)当t为何值时,△ABC的一边所在的直线与半圆O所在的圆相切?
(2)当△ABC的一边所在的直线与半圆O所在圆相切时,如果半圆O与直线MN围成的区域与△ABC三边围成的区域有重叠部分,求重叠部分的面积.
参考答案:
【答案】(1)1s、4s、7s、16s;(2) ![]()
【解析】试题分析:
(1)结合题意可知,本题存在四种可能,故分以下四种情况讨论计算即可:①如图1,圆O在直线AC左侧和直线AC相切;②如图2,圆O和直线AB左侧和直线AB相切;③如图3,圆O在直线AC右侧和直线AC相切;④如图4,圆O在直线AB右侧和直线AB相切;
(2)由(1)可知,在图2和图3的情形中,半圆O和△ABC有重叠部分,按图分情况计算即可.
试题解析:
(1)①如图1所示:当点N与点C重合时,AC⊥OC,OC=ON=3cm,
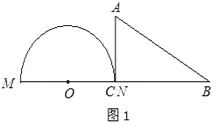
∴AC与半圆O所在的圆相切.
∴此时点O运动了1cm,故运动时间为:t=1(s)
②如图2所示;
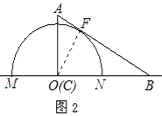
当点O运动到点C时,过点O作OF⊥AB,垂足为F.
∵在Rt△FOB中,∠FBO=30°,OB=6cm,
∴OF=3cm,即OF等于半圆O的半径,
∴AB与半圆O所在的圆相切.
此时点O运动了4cm,故运动时间为:t=4(s)
③如图3所示;过点O作OH⊥AB,垂足为H.
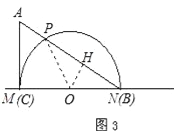
当点O运动到BC的中点时,AC⊥OC,OC=OM=3cm,
∴AC与半圆O所在的圆相切.
此时点O运动了7cm,故运动时间为:t=7(s).
④如图4所示;

当点O运动到B点的右侧,且OB=6cm时,过点O作OQ⊥AB,垂足为Q.
∵在Rt△QOB中,∠OBQ=30°,
∴OQ=![]() OB=3cm,即OQ等于半圆O所在的圆的半径,
OB=3cm,即OQ等于半圆O所在的圆的半径,
∴直线AB与半圆O所在的圆相切.
此时点O运动了16cm,所求运动时间为:t=16(s).
综上所述:当点![]() 的值为1s,4s,7s,16s时,半圆O所在圆和△ABC的边所在直线相切.
的值为1s,4s,7s,16s时,半圆O所在圆和△ABC的边所在直线相切.
(2)当△ABC的一边所在的直线与半圆O所在的圆相切时,半圆O与直径DE围成的区域与△ABC三边围成的区域有重叠部分的只有如图2与3所示的两种情形.
①如图2所示:重叠部分是圆心角为90°,半径为3cm的扇形,所求重叠部分面积=![]() (cm2);
(cm2);
②如图③所示:
设AB与半圆O的交点为P,连接OP,过点O作OH⊥AB,垂足为H.
则PH=BH.
∵在Rt△OBH中,∠OBH=30°,OB=3cm
∴OH=1.5cm,BH=![]() cm,BP=
cm,BP=![]() cm,
cm,
∴S△POB=![]() BP
BP![]() OH=
OH=![]() (cm2).
(cm2).
又∵∠DOP=2∠DBP=60°,
∴S扇形DOP=![]() (cm2),
(cm2),
∴所求重叠部分面积为:S△POB+S扇形DOP=![]() (cm2).
(cm2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A(-3,-2)向上平移2个单位,再向右平移2个单位到点B,则点B的坐标为( )
A. (1,0)B. (﹣1,0)C. (1,﹣4)D. (﹣5,﹣1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个完全相同的正四面体骰子的各面上分别标明数字1,2,3,4,在桌子上同时投掷这两个正四面体骰子,请用列表法或画树状图的方法,求与桌面接触的面所得的点数之和等于6的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次
第二次
第三次
第四次
第五次
第六次
甲
10
8
9
8
10
9
乙
10
7
10
10
9
8
(1)根据表格中的数据,分别计算甲、乙的平均成绩;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加省比赛更合适,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列从左到右的变形,是分解因式的是( )
A. xy2(x-1)=x2y2-xy2 B. x2+x-5=(x-2)(x+3)+1
C. (a+3)(a-3)=a2-9 D. 2a2+4a=2a(a+2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某旅行社的一则广告如下:我社推出去井冈山红色旅游,收费标准为:如果组团人数不超过30人,人均收费800元;如果人数多于30人,那么每增加1人,人均收费降低10元,但人均收费不得低于500元,甲公司想分批组织员工到井冈山红色旅游学习.
(1)如果第一批组织38人去学习,则公司应向旅行社交费 元;
(2)如果公司计划用29250元组织第一批员工去学习,问这次旅游学习应安排多少人参加?
-
科目: 来源: 题型:
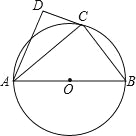
查看答案和解析>>【题目】如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.
(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.
相关试题

