【题目】一辆出租车从A地出发,在一条东西走向的街道上往返,每次行驶的情况(记向东为正)记录如下(x>5且x<14,单位:m):
行驶次数 | 第一次 | 第二次 | 第三次 | 第四次 |
行驶情况 | x | ﹣ | x﹣3 | 2(5﹣x) |
行驶方向(填“东”或“西”) |
|
|
|
|
(1)请将表格补充完整;
(2)求经过连续4次行驶后,这辆出租车所在的位置;
(3)若出租车行驶的总路程为41m,求第一次行驶的路程x的值.
参考答案:
【答案】(1)东,西,东,西;(2)向东(7﹣x)km;(3)12.
【解析】
(1)根据数的符号说明即可;
(2)把路程相加,求出结果,看结果的符号即可判断出答案;
(3)求出每个数的绝对值,相加求出总路程,再解方程求解即可.
解:(1)填表如下:
行驶次数 | 第一次 | 第二次 | 第三次 | 第四次 |
行驶情况 | x | ﹣ | x﹣3 | 2(5﹣x) |
行驶方向(填“东”或“西”) | 东 | 西 | 东 | 西 |
故答案为:东,西,东,西;
(2)x+(﹣![]() x)+(x﹣3)+2(5﹣x)=7﹣
x)+(x﹣3)+2(5﹣x)=7﹣![]() x,
x,
∵x>5且x<14,
∴7﹣![]() x>0,
x>0,
∴经过连续4次行驶后,这辆出租车所在的位置是向东(7﹣x)km.
(3)|x|+|﹣![]() x|+|x﹣3|+|2(5﹣x)|=x+
x|+|x﹣3|+|2(5﹣x)|=x+![]() x+x﹣3﹣2(5﹣x)=
x+x﹣3﹣2(5﹣x)=![]() x﹣13,
x﹣13,
依题意有![]() x﹣13=41,
x﹣13=41,
解得x=12.
答:第一次行驶的路程x的值是12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(阅读材料)小白同学在研究有理数分类时,认为“所有的无限循环小数都可以化为分数”,例如,
 怎样化成分数?
怎样化成分数?小白的思路是这样的:
设
 =x,则10×
=x,则10× =10x即
=10x即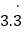 =10x,
=10x,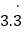 ﹣
﹣ =10x﹣x,3=9x,x=
=10x﹣x,3=9x,x=
(解决问题)请你按照小白的思路解决下列问题:
(1)将
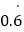 化成分数;
化成分数;(2)将
 化成分数.
化成分数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(1,6)和点B在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
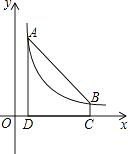
(1)求反比例函数的表达式和点B的坐标;
(2)连接AB,在线段DC上是否存在一点E,使△ABE的面积等于5?若存在,求出点E的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】(阅读)数轴上点A、B表示的数分别是a、b,若a>b,则AB=a﹣b.

例如,若数轴上点A、B表示的两个数分别为﹣2000和+18,
则AB=18﹣(﹣2000)=18+2000=2018
(应用)若数轴上点A、B表示的两个数分别为x和﹣1,且x>﹣1,则AB= (用含x的代数式表示);
(拓展)如图,数轴上点A表示的数为﹣2a,点B表示的数为﹣
 a,点C表示的数为﹣2,且AB=BC.
a,点C表示的数为﹣2,且AB=BC.(1)求a的值;
(2)以BC为边作等边三角形BCD,并将共向右滚动1周得到新的等边三角形BCD,依次继续滚动…….若滚动第n周后,等边三角形BCD的顶点C表示的数是2014,求n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为4cm的正方形ABCD绕点S顺时针旋转到四边形AB′C′D′的位置,旋转角为30°,则C点运动到C′点的路径长为( )
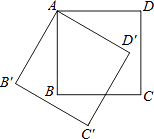
A. πcm
πcm
B.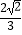 πm
πm
C.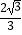 cm
cm
D.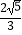 cm
cm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个在平面直角坐标系中从原点开始的回形图,其中回形通道的宽和OA的长都是1.
(1)观察图形填写表格:
点
坐标
所在象限或坐标轴
A
B
C
D
E
F

(2)在图上将回形图继续画下去(至少再画出4个拐点);
(3)说出回形图中位于第一象限的拐点的横坐标与纵坐标之间的关系;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则
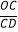 的值为( )
的值为( ) 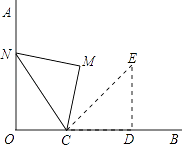
A.
B.
C.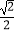
D.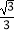
相关试题

