搜索
【题目】已知互不相等的实数m、n，且满足m2+3m﹣5＝0，n2+3n﹣5＝0，则m2﹣n2+mn+6m的值为（ ）
A.14B.﹣14C.10D.﹣10
参考答案：
【答案】B
【解析】
根据根与系数的关系即可求出答案．
解：由题意可知：m、n是方程x2+3x﹣5＝0的两根，
∴m+n＝﹣3，mn＝﹣5，
∴原式＝（m+n）（m﹣n）+mn+6m
＝﹣3（m﹣n）﹣5+6m
＝﹣3m+3n+6m﹣5
＝3m+3n﹣5
＝3（m+n）﹣5
＝﹣9﹣5
＝﹣14，
故选：B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知△ABC，∠C=90°，AC＜BC．D为BC上一点，且到A，B两点的距离相等．
（1）用直尺和圆规，作出点D的位置（不写作法，保留作图痕迹）；
（2）连接AD，若∠B=35°，求∠CAD的度数． -
科目： 来源： 题型：
查看答案和解析>>【题目】为了调查居民的生活水平，有关部门对某居委会的50户居民的家庭存款额进行了调查，数据（单位：万元）如下：
1.7 3.5 2.3 6.4 2.0 1.9 6.7 4.8 5.0 4.7
2.3 3.4 5.6 3.7 2.2 3.3 5.8 4.3 3.6 3.8
3.0 5.1 7.0 3.1 2.9 4.9 5.8 3.6 3.0 4.2
4.0 3.9 5.1 6.3 1.8 3.2 5.1 5.7 3.9 3.1
2.5 2.8 4.5 4.9 5.3 2.6 7.2 1.9 5.0 3.8
（1）这50个家庭存款额的最大值、最小值分别是多少？它们相差多少？
（2）填表：存款额x（万元）
划记
户数
1.0≤x＜2.0
2.0≤x＜3.0
3.0≤x＜4.0
4.0≤x＜5.0
5.0≤x＜6.0
6.0≤x＜7.0
7.0≤x＜8.0
（3）根据上表谈谈这50户家庭存款额的分布情况． -
科目： 来源： 题型：
查看答案和解析>>【题目】二次函数y＝﹣x2+2x+4的顶点坐标是（ ）
A.（﹣1，5）B.（1，5）C.（﹣1，﹣5）D.（1，﹣5）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在一次测量活动中，小丽站在离树底部E处5m的B处仰望树顶C，仰角为30°，已知小丽的眼睛离地面的距离AB为1.65m，那么这棵树大约有多高？（结果精确到0.1m，参考数据：
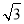≈1.73）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将△ABC沿着过AB中点D的直线折叠，使点A落在BC边上的A2处，称为第1次操作，折痕DE到BC的距离记为h1；还原纸片后，再将△ADE沿着过AD中点D1的直线折叠，使点A落在DE边上的A2处，称为第2次操作，折痕D1E1到BC的距离记为h2；按上述方法不断操作下去…，经过第2015次操作后得到的折痕D2014E2014到BC的距离记为h2015，到BC的距离记为h2015．若h1=1，则h2015的值为（ ）
A．
B．
C．
D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法中，正确的个数为：①在等圆中，等弦对等弧；②直径是圆的对称轴；③平分弦的直径垂直于这条弦；④弦的中垂线一定经过圆心．（ ）
A.0B.1C.2D.3
相关试题
