【题目】为了调查居民的生活水平,有关部门对某居委会的50户居民的家庭存款额进行了调查,数据(单位:万元)如下:
1.7 3.5 2.3 6.4 2.0 1.9 6.7 4.8 5.0 4.7
2.3 3.4 5.6 3.7 2.2 3.3 5.8 4.3 3.6 3.8
3.0 5.1 7.0 3.1 2.9 4.9 5.8 3.6 3.0 4.2
4.0 3.9 5.1 6.3 1.8 3.2 5.1 5.7 3.9 3.1
2.5 2.8 4.5 4.9 5.3 2.6 7.2 1.9 5.0 3.8
(1)这50个家庭存款额的最大值、最小值分别是多少?它们相差多少?
(2)填表:
存款额x(万元) | 划记 | 户数 |
1.0≤x<2.0 |
| |
2.0≤x<3.0 |
| |
3.0≤x<4.0 |
| |
4.0≤x<5.0 |
| |
5.0≤x<6.0 |
| |
6.0≤x<7.0 |
| |
7.0≤x<8.0 |
|
(3)根据上表谈谈这50户家庭存款额的分布情况.
参考答案:
【答案】
(1)解:存款额的最大值为7.2万元,存款额的最小值为1.7万元,相差:7.2﹣1.7=5.5(万元)
(2)4,8,15,8,10,3,2
(3)解:由表可得,这50户家庭中,存款额在2.0≤x<6.0范围内的户数较多,其中在3.0≤x<4.0范围内的户数最多,而存款额在1.0≤x<2.0,6.0≤x<8.0范围内户数较少,占小部分
【解析】解:(2)根据划记可得,1.0≤x<2.0一组的户数为4,2.0≤x<3.0一组的户数为8,3.0≤x<4.0一组的户数为15,4.0≤x<5.0一组的户数为8,5.0≤x<6.0一组的户数为10,6.0≤x<7.0一组的户数为3,7.0≤x<8.0一组的户数为2;
所以答案是:4,8,15,8,10,3,2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=﹣x+4与两坐标轴分别相交于点A,B两点,点C是线段AB上任意一点,过C分别作CD⊥x轴于点D,CE⊥y轴于点E.双曲线
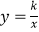 与CD,CE分别交于点P,Q两点,若四边形ODCE为正方形,且
与CD,CE分别交于点P,Q两点,若四边形ODCE为正方形,且 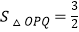 ,则k的值是( )
,则k的值是( )
A.4
B.2
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=(x﹣2)2+1的顶点坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,∠C=90°,AC<BC.D为BC上一点,且到A,B两点的距离相等.

(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连接AD,若∠B=35°,求∠CAD的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=﹣x2+2x+4的顶点坐标是( )
A.(﹣1,5)B.(1,5)C.(﹣1,﹣5)D.(1,﹣5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知互不相等的实数m、n,且满足m2+3m﹣5=0,n2+3n﹣5=0,则m2﹣n2+mn+6m的值为( )
A.14B.﹣14C.10D.﹣10
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一次测量活动中,小丽站在离树底部E处5m的B处仰望树顶C,仰角为30°,已知小丽的眼睛离地面的距离AB为1.65m,那么这棵树大约有多高?(结果精确到0.1m,参考数据:
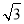 ≈1.73)
≈1.73)
相关试题

