【题目】在一次数学课上,老师出示了这样一道题目:“如图,BD是矩形ABCD的对角线,将AB沿BE折叠,使A点落在BD上的点G处,将边CD沿DF折叠,使点C落在BD上的点H处,求证:四边形BEDF是平行四边形”.小丽选择了先证明△DEG≌△BFH,再证明DE=BF,进而得到四边形BEDF是平行四边形,小明向老师提出了另一种证明方法.
(1)小丽证明四边形BEDF是平行四边形的依据是;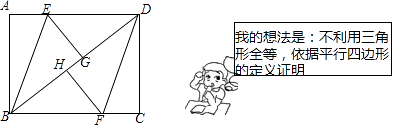
(2)按小明的想法写出证明过程;
(3)当学生们完成了证明后,老师又提出如下问题,连接EH,FG,若AB=6,BC=8,试求四边形EGFH的周长.
参考答案:
【答案】
(1)一组对边平行且相等的四边形是平行四边形
(2)证明:由翻折的性质可知:∠ABE=∠DBE═ ![]() ,EG=EA,FH=FC
,EG=EA,FH=FC
∠BDF═∠CDF= ![]() .
.
又∵四边形ABCD是矩形,
∴AD∥BC,AB∥CD,
∴∠ABD=∠CDB,
∴∠DBE=∠BDF,
∴BE∥DF,
又DE∥BF,
∴四边形BEDF是平行四边形(两组对边分别平行的四边形是平行四边形);
(3)解:连接EH、GF,如图所示:
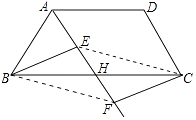
∵∠A=90°,AD=BC=8,AB=6,GB=AB=6,
∴BD= ![]() =10,
=10,
∴DG=BD﹣GB=4,
设AE=x,则DE=8﹣x,EG=AE=x,
在Rt△DGE中,由勾股定理得(8﹣x)2=x2+42,
解得x=3,
∴AE=3,
同理FH=3,
由(1)得:EG=FH,
∵EG⊥BD,FH⊥BD,
∴EG∥FH,
∴四边形EGFH是平行四边形,EG=FH=3,
∵BG=DH=6,
∴DG=BH=4,
∴GH=2,
在Rt△EGH中, ![]() ,
,
四边形EGFH的周长为 ![]() .
.
【解析】(1)解:一组对边平行且相等的四边形是平行四边形;理由如下:
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,AB∥CD,∠A=∠C=90°,
∴∠EDG=∠FBH,
由折叠的性质得:∠EGB=∠A=90°,GB=AB,HD=CD,
∴∠DGE=∠BHF=90°,DG=BH,
在△DEG和△BFH中, 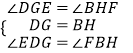 ,
,
∴△DEG≌△BFH(ASA),
∴DE=BF,
又∵DE∥BF,
∴四边形BEDF是平行四边形;
所以答案是:一组对边平行且相等的四边形是平行四边形;
【考点精析】根据题目的已知条件,利用平行四边形的判定与性质的相关知识可以得到问题的答案,需要掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学今年年初开学后打算招聘一名数学老师,对三名前来应聘的数学老师A、B、C进行了考核,他们的笔试成绩和说课成绩(单位:分)分别用了两种方式进行了统计,如表和图1,
A
B
C
笔试
85
95
90
说课
80
85
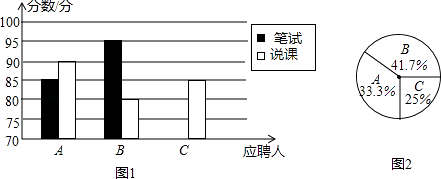
(1)请将表和图1的空缺部分补充完整;
(2)应聘的最后一个程序是由该校的24名数学教师进行投票,三位应聘者的得票情况如图2(没有弃权票,该校的每位教师只能选一位应聘教师),请计算每人的得票数(得票数可是整数哟)
(3)若每票计1分,该校将笔试、说课、得票三项测试得分按3:4:3的比例 确定个人成绩,请计算三位应聘者的最后成绩,并根据成绩判断谁能应聘成功. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为r,圆心O到直线l的距离为d.若直线l与⊙O有交点,则下列结论正确的是( )
A.d=rB.d≤rC.d≥rD.d<r
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知(2x2﹣3x+a)(x+2)计算结果中不含x的一次项,则a=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:

(1)甲登山上升的速度是每分钟米,乙在A地时距地面的高度b为米.
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式.
(3)登山多长时间时,甲、乙两人距地面的高度差为50米? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三角形ABC内任意一点P(x0,y0),将三角形ABC平移后,点P的对应点为P1(x0+5,y0-3).
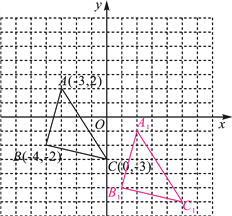
(1)写出将三角形ABC平移后,三角形ABC中A,B,C分别对应的点A1,B1,C1的坐标,并画出三角形A1B1C1;
(2)若三角形ABC外有一点M经过同样的平移后得到点M1(5,3),写出M点的坐标_______,若连接线段MM1,PP1,则这两条线段之间的关系是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某数学兴趣小组在数学课外活动中,研究三角形和正方形的性质时,做了如下探究:
在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时,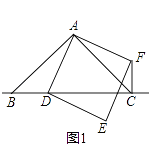
①BC与CF的位置关系为: ,
②BC,DC,CF之间的数量关系为:;(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,(1)中的①,②结论是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.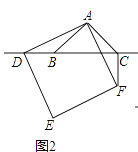
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2,CD=BC,请直接写出GE的长.
相关试题

