【题目】已知AB是⊙O的直径,点P在弧AB上(不含点A、B),把△AOP沿OP对折,点A的对应点C恰好落在⊙O上.

(1)当P、C都在AB上方时(如图1),判断PO与BC的位置关系(只回答结果);
(2)当P在AB上方而C在AB下方时(如图2),(1)中结论还成立吗?证明你的结论;
(3)当P、C都在AB上方时(如图3),过C点作CD⊥直线AP于D,且CD是⊙O的切线,求证:AB=4PD.
参考答案:
【答案】(1)PO∥BC;(2)成立,理由详见解析;(3)详见解析.
【解析】试题分析:(1)PO与BC的位置关系是平行;
(2)中的结论成立,理由为:由折叠可知三角形APO与三角形CPO全等,根据全等三角形的对应角相等可得出∠APO=∠CPO,再由OA=OP,利用等边对等角得到∠A=∠APO,等量代换可得出∠A=∠CPO,又根据同弧所对的圆周角相等得到∠A=∠PCB,再等量代换可得出∠CPO=∠PCB,利用内错角相等两直线平行,可得出PO与BC平行;
(3)由CD为圆O的切线,利用切线的性质得到OC垂直于CD,又AD垂直于CD,利用平面内垂直于同一条直线的两直线平行得到OC与AD平行,根据两直线平行内错角相等得到∠APO=∠COP,再利用折叠的性质得到∠AOP=∠COP,等量代换可得出∠APO=∠AOP,再由OA=OP,利用等边对等角可得出一对角相等,等量代换可得出三角形AOP三内角相等,确定出三角形AOP为等边三角形,根据等边三角形的内角为60°得到∠AOP为60°,由OP平行于BC,利用两直线平行同位角相等可得出∠OBC=∠AOP=60°,再由OB=OC,得到三角形OBC为等边三角形,可得出∠COB为60°,利用平角的定义得到∠POC也为60°,再加上OP=OC,可得出三角形POC为等边三角形,得到内角∠OCP为60°,可求出∠PCD为30°,在直角三角形PCD中,利用30°所对的直角边等于斜边的一半可得出PD为PC的一半,而PC等于圆的半径OP等于直径AB的一半,可得出PD为AB的四分之一,即AB=4PD,得证.
试题解析:(1)PO与BC的位置关系是PO∥BC;
(2)(1)中的结论PO∥BC成立,理由为:由折叠可知:△APO≌△CPO,
∴∠APO=∠CPO,又∵OA=OP,∴∠A=∠APO,∴∠A=∠CPO,
又∵∠A与∠PCB都为![]() 所对的圆周角,∴∠A=∠PCB,∴∠CPO=∠PCB,
所对的圆周角,∴∠A=∠PCB,∴∠CPO=∠PCB,
∴PO∥BC;
(3)∵CD为圆O的切线,∴OC⊥CD,又AD⊥CD,∴OC∥AD,∴∠APO=∠COP,
由折叠可得:∠AOP=∠COP,∴∠APO=∠AOP,又OA=OP,∴∠A=∠APO,
∴∠A=∠APO=∠AOP,∴△APO为等边三角形,∴∠AOP=60°,又∵OP∥BC,
∴∠OBC=∠AOP=60°,又OC=OB,∴△BCO为等边三角形,∴∠COB=60°,
∴∠POC=180°﹣(∠AOP+∠COB)=60°,又OP=OC,
∴△POC也为等边三角形,
∴∠PCO=60°,PC=OP=OC,
又∵∠OCD=90°,
∴∠PCD=30°,
在Rt△PCD中,PD=![]() PC,
PC,
又∵PC=OP=![]() AB,
AB,
∴PD=![]() AB,即AB=4PD.
AB,即AB=4PD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知点E(﹣4,2),F(﹣2,﹣2),以原点O为位似中心,位似比为2:1将△EFO缩小,则点E的对应点E′的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知菱形A1B1C1D1的边长为2,∠A1B1C1=60°,对角线A1C1,B1D1相交于点O.以点O为坐标原点,分别以OA1,OB1所在直线为x轴、y轴,建立如图所示的直角坐标系.以B1D1为对角线作菱形B1C2D1A2∽菱形A1B1C1D1,再以A2C2为对角线作菱形A2B2C2D2∽菱形B1C2D1A2,再以B2D2为对角线作菱形B2C3D2A3∽菱形A2B2C2D2,…,按此规律继续作下去,在x轴的正半轴上得到点A1,A2,A3,…,An,则点An的坐标为____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,有一张矩形纸片ABCD,E、F分别是BC、AD上的点(不与顶点重合).如果直线EF将矩形分成面积相等的两部分,那么
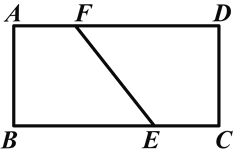
(1)得到的两个四边形是否相似?若相似,请求出相似比;若不相似,请说明理由;
(2)这样的直线可以作多少条?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算5﹣(﹣2)×3的结果等于( )
A.﹣11
B.﹣1
C.1
D.11 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,且AB =6,C是⊙O上一点,D是
 的中点,过点D作⊙O的切线,与AB、AC的延长线分别交于点E、F,连接AD.
的中点,过点D作⊙O的切线,与AB、AC的延长线分别交于点E、F,连接AD.
(l)求证:AF⊥EF;
(2)填空:
①当BE= 时,点C是AF的中点;
②当BE= 时,四边形OBDC是菱形,
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC边于点D,过点C作CF∥AB,与过点B的切线交于点F,连接BD.
(1)求证:BD=BF;
(2)若AB=10,CD=4,求BC的长.

相关试题

