【题目】如图,MN是⊙O的直径,MN=4,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )
A.2
B.2 ![]()
C.2 ![]()
D.3
参考答案:
【答案】C
【解析】解:过A作关于直线MN的对称点A′,连接A′B,由轴对称的性质可知A′B即为PA+PB的最小值,
连接OB,OA′,AA′,
∵AA′关于直线MN对称,
∴ ![]() =
= ![]() ,
,
∵∠AMN=40°,
∴∠A′ON=80°,∠BON=40°,
∴∠A′OB=120°,
过O作OQ⊥A′B于Q,
在Rt△A′OQ中,OA′=2,
∴A′B=2A′Q=2 ![]() ,
,
即PA+PB的最小值2 ![]() .
.
故选C.
【考点精析】掌握圆周角定理和轴对称-最短路线问题是解答本题的根本,需要知道顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程(m﹣2)2x2+(2m+1)x+1=0有两个不相等的实数根,则m的取值范围是( )
A.m<
B.m> 且m≠2
且m≠2
C.m≤
D.m≥ 且m≠2
且m≠2 -
科目: 来源: 题型:
查看答案和解析>>【题目】为调动销售人员的积极性,A、B两公司采取如下工资支付方式:A公司每月2000元基本工资,另加销售额的2%作为奖金;B公司每月1600元基本工资,另加销售额的4%作为奖金。已知A、B公司两位销售员小李、小张1~6月份的销售额如下表:

(1)请问小李与小张3月份的工资各是多少?
(2)小李1~6月份的销售额
 与月份
与月份 的函数关系式是
的函数关系式是 小张1~6月份的销售额
小张1~6月份的销售额 也是月份
也是月份 的一次函数,请求出
的一次函数,请求出 与
与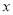 的函数关系式;
的函数关系式;(3)如果7~12月份两人的销售额也分别满足(2)中两个一次函数的关系,问几月份起小张的工资高于小李的工资。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法不正确的是( )
A.某种彩票中奖的概率是 ,买1000张该种彩票一定会中奖
,买1000张该种彩票一定会中奖
B.了解一批电视机的使用寿命适合用抽样调查
C.若甲组数据的标准差S甲=0.31,乙组数据的标准差S乙=0.25,则乙组数据比甲组数据稳定
D.在一个装有白球和绿球的袋中摸球,摸出黑球是不可能事件 -
科目: 来源: 题型:
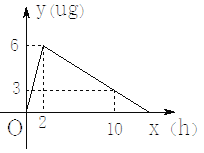
查看答案和解析>>【题目】某医药研究生开发了一种新药,在实验药效时发现,如果成人按规剂量服用,那么服用药后2h时血液中含药量最高,达每毫升6ug,接着逐步衰减,10h时血液中含药量每毫升3ug,每毫升血液中含药量y(ug)随时间x(h)的变化如图所示,当成人按规定剂量服药后.
(1)分别求出x≤2和x>2时,y与x之间的函数关系式;
(2)如果每毫升血液含药量为4ug或4ug以上时在治疗疾病时是有效的,那么这个有效时间是多长?每天至少吃几次药疗效最好?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线L1过A(0,2),B(2,0)两点,直线L2:y=mx+b过点C(1,0),且把△AOB分成两部分,其中靠近原点的那部分是一个三角形,设此三角形的面积为S,求S关于m的函数解析式,及自变量m的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,  ,
,  、
、 是腰
是腰 、
、 上的高,交于点
上的高,交于点 .
.(
 )求证:
)求证:  .
.(
 )若
)若 ,求
,求 的度数.
的度数.
相关试题

