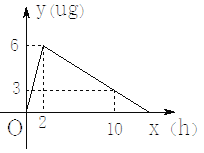
【题目】某医药研究生开发了一种新药,在实验药效时发现,如果成人按规剂量服用,那么服用药后2h时血液中含药量最高,达每毫升6ug,接着逐步衰减,10h时血液中含药量每毫升3ug,每毫升血液中含药量y(ug)随时间x(h)的变化如图所示,当成人按规定剂量服药后.
(1)分别求出x≤2和x>2时,y与x之间的函数关系式;
(2)如果每毫升血液含药量为4ug或4ug以上时在治疗疾病时是有效的,那么这个有效时间是多长?每天至少吃几次药疗效最好?
参考答案:
【答案】(1)x≤2时解析式为y=3x(0≤x≤2);x>2时,解析式为y=-![]() x+
x+![]() (x>2);
(x>2);
(2)有效时间为6(小时),每天至少吃4(次).
【解析】试题分析:(1)根据图象写出函数解析式,前面2h对应的线段是正比例函数的图象,设为y=k1x(k1≠0),把(2,6)代入即可求出k1.当x>2时,图象对应的是一次函数,设为y=k2x+b(k2≠0).把(2,6),(10,3)代入即可求出k2,b;
(2)由图象可知,有两个时刻成人血液中的含药量为4μg,这两个时刻间的时间段内含药量高于4μg,通过计算即可得.
试题解析:(1)设x≤2和x>2时,y与x之间的函数关系式分别为y=k1x,y=k2x+b,
将点(2,6)代入y=k1x,解得k1=3,
将点(2,6)(10,3)代入y=k2x+b,则6=2k2+b,3=10k2+b,
解得k2=-![]() ,b=
,b=![]() ,
,
即x≤2时解析式为y=3x(0≤x≤2),x>2时,解析式为y=-![]() x+
x+![]() (x>2);
(x>2);
(2)将y=4,分别代入上述两个解析式,4=3x,解得x=![]() ,
,
4=-![]() x+
x+![]() ,解得x=
,解得x=![]() ,
,
故有效时间为![]() -
-![]() =6(小时),
=6(小时),
每天至少吃24÷6=4(次).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为调动销售人员的积极性,A、B两公司采取如下工资支付方式:A公司每月2000元基本工资,另加销售额的2%作为奖金;B公司每月1600元基本工资,另加销售额的4%作为奖金。已知A、B公司两位销售员小李、小张1~6月份的销售额如下表:

(1)请问小李与小张3月份的工资各是多少?
(2)小李1~6月份的销售额
 与月份
与月份 的函数关系式是
的函数关系式是 小张1~6月份的销售额
小张1~6月份的销售额 也是月份
也是月份 的一次函数,请求出
的一次函数,请求出 与
与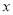 的函数关系式;
的函数关系式;(3)如果7~12月份两人的销售额也分别满足(2)中两个一次函数的关系,问几月份起小张的工资高于小李的工资。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法不正确的是( )
A.某种彩票中奖的概率是 ,买1000张该种彩票一定会中奖
,买1000张该种彩票一定会中奖
B.了解一批电视机的使用寿命适合用抽样调查
C.若甲组数据的标准差S甲=0.31,乙组数据的标准差S乙=0.25,则乙组数据比甲组数据稳定
D.在一个装有白球和绿球的袋中摸球,摸出黑球是不可能事件 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,MN是⊙O的直径,MN=4,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )

A.2
B.2
C.2
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线L1过A(0,2),B(2,0)两点,直线L2:y=mx+b过点C(1,0),且把△AOB分成两部分,其中靠近原点的那部分是一个三角形,设此三角形的面积为S,求S关于m的函数解析式,及自变量m的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,  ,
,  、
、 是腰
是腰 、
、 上的高,交于点
上的高,交于点 .
.(
 )求证:
)求证:  .
.(
 )若
)若 ,求
,求 的度数.
的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了奖励优秀班集体,学校购买了若干副乒乓球拍和羽毛球拍,购买2副乒乓球拍和1副羽毛球拍共需116元,购买3幅乒乓球拍和2幅羽毛球拍共需204元.
(1)每副乒乓球拍和羽毛球拍的单价各是多少元?
(2)若学校购买5副乒乓球拍和3副羽毛球拍,一共应支出多少元?
相关试题

