【题目】已知抛物线c1的顶点为A(﹣1,4),与y轴的交点为D(0,3).
(1)求c1的解析式;
(2)若直线l1:y=x+m与c1仅有唯一的交点,求m的值;
(3)若抛物线c1关于y轴对称的抛物线记作c2,平行于x轴的直线记作l2:y=n.试结合图形回答:当n为何值时,l2与c1和c2共有:①两个交点;②三个交点;③四个交点;
(4)若c2与x轴正半轴交点记作B,试在x轴上求点P,使△PAB为等腰三角形.

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)①4;②3;③3<n<4或n<3;(4)(﹣5,0)或(3﹣
;(3)①4;②3;③3<n<4或n<3;(4)(﹣5,0)或(3﹣![]() ,0)或(3+
,0)或(3+![]() ,0)或(﹣1,0).
,0)或(﹣1,0).
【解析】
试题分析:(1)设抛物线c1的解析式为![]() ,把D(0,3)代入
,把D(0,3)代入![]() 即可得到结论;
即可得到结论;
(2)解方程组得到![]() ,由于直线l1:y=x+m与c1仅有唯一的交点,于是得到△=9﹣4m+12=0,即可得到结论;
,由于直线l1:y=x+m与c1仅有唯一的交点,于是得到△=9﹣4m+12=0,即可得到结论;
(3)根据轴对称的性质得到抛物线c2的解析式为:![]() ,根据图象即可刚刚结论;
,根据图象即可刚刚结论;
(4)求得B(3,0),得到OB=3,根据勾股定理得到AB的长,①当AP=AB,②当AB=BP=![]() 时,③当AP=PB时,点P在AB的垂直平分线上,于是得到结论.
时,③当AP=PB时,点P在AB的垂直平分线上,于是得到结论.
试题解析:(1)∵抛物线c1的顶点为A(﹣1,4),∴设抛物线c1的解析式为![]() ,把D(0,3)代入
,把D(0,3)代入![]() 得3=a+4,∴a=﹣1,∴抛物线c1的解析式为:
得3=a+4,∴a=﹣1,∴抛物线c1的解析式为:![]() ,即
,即![]() ;
;
(2)解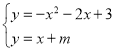 得
得![]() ,∵直线l1:y=x+m与c1仅有唯一的交点,∴△=9﹣4m+12=0,∴m=
,∵直线l1:y=x+m与c1仅有唯一的交点,∴△=9﹣4m+12=0,∴m=![]() ;
;
(3)∵抛物线c1关于y轴对称的抛物线记作c2,∴抛物线c2的顶点坐标为(1,4),与y轴的交点为(0,3),∴抛物线c2的解析式为:![]() ,∴①当直线l2过抛物线c1的顶点(﹣1,4)和抛物线记作c2的顶点(1,4)时,即n=4时,l2与c1和c2共有两个交点;
,∴①当直线l2过抛物线c1的顶点(﹣1,4)和抛物线记作c2的顶点(1,4)时,即n=4时,l2与c1和c2共有两个交点;
②当直线l2过D(0,3)时,即n=3时,l2与c1和c2共有三个交点;
③当3<n<4或n<3时,l2与c1和c2共有四个交点;
(4)如图,∵若c2与x轴正半轴交于B,∴B(3,0),∴OB=3,∴AB=![]() =
=![]() :
:
①当AP=AB=![]() 时,PB=8,∴P1(﹣5,0);
时,PB=8,∴P1(﹣5,0);
②当AB=BP=![]() 时,P2(3﹣
时,P2(3﹣![]() ,0)或P3(3+
,0)或P3(3+![]() ,0);
,0);
③当AP=PB时,点P在AB的垂直平分线上,∴PA=PB=4,∴P4(﹣1,0).
综上所述,点P的坐标为(﹣5,0)或(3﹣![]() ,0)或(3+
,0)或(3+![]() ,0)或(﹣1,0)时,△PAB为等腰三角形.
,0)或(﹣1,0)时,△PAB为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.
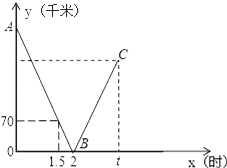
(1)根据图中信息,求线段AB所在直线的函数解析式和甲乙两地之间的距离;
(2)已知两车相遇时快车比慢车多行驶40千米,若快车从甲地到达乙地所需时间为t时,求t的值;
(3)在(2)的条件下,若快车到达乙地后立刻返回甲地,慢车到达甲地后停止行驶,请你在图中画出快车从乙地返回到甲地过程中y关于x的函数的大致图象. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,正确的是( )
A.5a+3b=8abB.4a3+2a2=6a5
C.8b2﹣7b2=1D.6ab2﹣6b2a=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a=-2×32,b=(-2×3)2,c=-(2×3)2,将a,b,c三个数用“<”连接起来应为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a+b=2,则a2-b2+4b的值是( )
A. 2B. 3C. 4D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b=ab2﹣2ab+b.如:2☆(﹣3)=2×(﹣3)2﹣2×2×(﹣3)+(﹣3)=27.依据此定义化简(1﹣3x)☆(﹣4)=____.
-
科目: 来源: 题型:
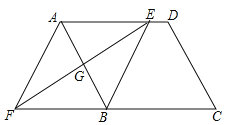
查看答案和解析>>【题目】如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE.
(1)求证:△AGE≌△BGF;
(2)试判断四边形AFBE的形状,并说明理由.
相关试题

