【题目】一辆快车从甲地驶往乙地，一辆慢车从乙地驶往甲地，两车同时出发，匀速行驶设行驶的时间为x（时），两车之间的距离为y（千米），图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系．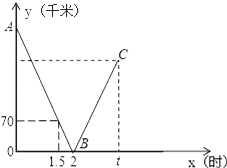

（1）根据图中信息，求线段AB所在直线的函数解析式和甲乙两地之间的距离；
（2）已知两车相遇时快车比慢车多行驶40千米，若快车从甲地到达乙地所需时间为t时，求t的值；
（3）在（2）的条件下，若快车到达乙地后立刻返回甲地，慢车到达甲地后停止行驶，请你在图中画出快车从乙地返回到甲地过程中y关于x的函数的大致图象．

参考答案：

【答案】
（1）解：设 的解析式为

将 ， 代入得

的解析式为

即甲、乙两地距离为


（2）解：设相遇时慢车走的路程为

则快车路程为

快车行驶路程为

由图可知， 小时两车相遇

快车速度


（3）解：慢车速度：

从乙地到甲地共需

此时，甲、乙相距

图象如图所示


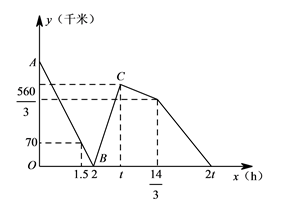
【解析】（1）根据图像可知直线AB经过( 1.5,70 ) ， (2,0)，设函数解析式，利用待定系数法求出此函数解析式，再求出点A的坐标，即可求出甲乙两地之间的距离。
（2）设相遇时慢车走的路程为 S,则快车行驶的路程为S+40，根据两车相遇路程之和=总路程，就可求出快车行驶的路程，观察函数图像可知2小时相遇，即可求出快车的速度，然后根据路程除以速度，即可求出快车从甲地到达乙地所需时间。
（3）先求出慢车的速度及慢车从乙地到甲地共需的时间，再求出此时甲乙相距的路程，然后画出快车从乙地返回到甲地过程中y关于x的函数的大致图象。

关闭