【题目】已知![]() ,求
,求![]() 的最大值与最小值.
的最大值与最小值.
参考答案:
【答案】x+y最大值为6,最小值为-3.
【解析】
先将|x+2|+|1-x|=9-|y-5|-|1+y|化为|x+2|+|1-x|+|y-5|+|1+y|=9.再对x、y的取值进行分类讨论:当x≥1,y≥5时;当1>x≥-2,5>y≥-1时;当x<-2,y<-1时.最后求出最大最小值.
|x+2|+|1-x|=9-|y-5|-|1+y|,
∴|x+2|+|1-x|+|y-5|+|1+y|=9,
当x≥1,y≥5时,x+2+x-1+y-5+y+1=9,
2x+2y=12 即x+y=6,
当1>x≥-2,5>y≥-1时,
x+2+1-x+5-y+y+1=9,但-3<x+y<6,
当x<-2,y<-1时,
-x-2+1-x+5-y-1-y=9,
得-2x-2y=6即 x+y=-3,
故x+y最大值为6,最小值为-3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AE⊥BD于E,CF⊥BD于F,连结AF,CE.求证:四边形AECF是平行四边形.
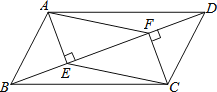
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AB=a,P为边BC上一动点(不与B、C重合),E是边BC延长线上一点,连结AP,过点P作PF⊥AP交∠DCE的平分线于点F,连结AF与边CD交于点G,连结PG.
猜想:线段PA与PF的数量关系为 .
探究:△CPG的周长在点P的运动中是否改变?若不改变求其值.
应用:若PG∥CF,当a=
 时,则PB= .
时,则PB= .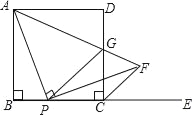
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在锐角△ABC中,AB=5,tanC=3,BD⊥AC于点D,BD=3,点P从点A出发,以每秒1个单位长度的速度沿AB向终点B运动,过点P作PE∥AC交边BC于点E,以PE为边作Rt△PEF,使∠EPF=90°,点F在点P的下方,且EF∥AB.设△PEF与△ABD重叠部分图形的面积为S(平方单位)(S>0),点P的运动时间为t(秒)(t>0).
(1)求线段AC的长.
(2)当△PEF与△ABD重叠部分图形为四边形时,求S与t之间的函数关系式.
(3)若边EF与边AC交于点Q,连结PQ,如图②.
①当PQ将△PEF的面积分成1:2两部分时,求AP的长.
②直接写出PQ的垂直平分线经过△ABC的顶点时t的值.
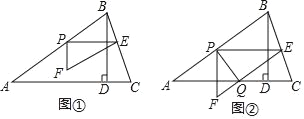
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P是正方形ABCD边AB上一点(不与A、B重合),连接PD并将线段PD绕点P顺时针旋转90°,得线段PE,连接BE,则∠CBE等于( )

A. 75°B. 60°C. 30°D. 45°
-
科目: 来源: 题型:
查看答案和解析>>【题目】
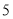 个有理数两两的乘积是如下
个有理数两两的乘积是如下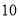 个数:
个数: ,
,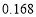 ,
,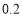 ,
,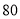 ,
,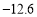 ,
,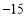 ,
,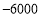 ,
,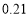 ,
,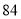 ,
,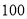 .请确定这
.请确定这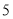 个数并简述理由.
个数并简述理由.
相关试题

