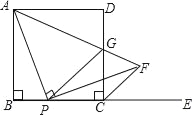
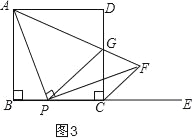
【题目】如图,在正方形ABCD中,AB=a,P为边BC上一动点(不与B、C重合),E是边BC延长线上一点,连结AP,过点P作PF⊥AP交∠DCE的平分线于点F,连结AF与边CD交于点G,连结PG.
猜想:线段PA与PF的数量关系为 .
探究:△CPG的周长在点P的运动中是否改变?若不改变求其值.
应用:若PG∥CF,当a=![]() 时,则PB= .
时,则PB= .
参考答案:
【答案】答案见解析.
【解析】试题分析:
(1)猜想:PA=PF,在在BA边上截取BQ=BP,连接PQ,如图1:
通过证:∠BAP=∠CPF,∠AQB=∠PCF,AQ=CP证得△AQP≌△PCF,即可得到PA=PF;
(2)△CPG的周长在点P的运动中不改变,是一个定值;理由如下:
如图2,延长CB至M,使BM=DG,连接AM,先证△ABM≌△ADG,再证△PAM≌△PAG,从而可得:△CPG的周长= PG+PC+CG=PM+PC+CG=PB+BM+PC+CG
=PB+DG+PC+CG=BC+DC=2AB=2a;
(3)由PG∥CF可证得△PCG是等腰直角三角形,从而可得PC=GC,PG=![]() PC,设PB=
PC,设PB= ![]() ,则PC=GC=
,则PC=GC= ![]() ,PG=
,PG=![]() ;结合(2)中结论可得:
;结合(2)中结论可得: ![]() ,结合
,结合![]() 解此的方程,即可得到PB的值.
解此的方程,即可得到PB的值.
试题解析:
(1)猜想:PA=PF,理由是:
在BA边上截取BQ=BP,连接PQ,如图1:
可得△BPQ为等腰直角三角形,即∠BQP=45°,
∴∠AQP=135°,
又∵CF为直角∠DCE的平分线,
∴∠FCE=45°,
∴∠PCF=∠AQP=135°,
∵四边形ABCD为正方形,
∴∠B=∠BCD=∠D=90°,AB=BC=CD,
∴AB﹣BQ=BC﹣BP,即AQ=PC,
∵PF⊥AP,
∴∠APF=90°,
∴∠APB+∠CPF=90°,
又∵∠APB+∠QAP=90°,
∴∠QAP=∠CPF,
在△AQP和△PCF中, 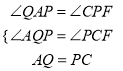 ,
,
∴△AQP≌△PCF(ASA),
∴PA=FP;
故答案为:PA=PF;
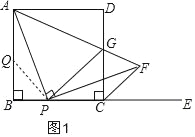
探究:△CPG的周长在点P的运动中不改变,是一个定值;
如图2,延长CB至M,使BM=DG,连接AM,
∵AD=AB,∠ABM=∠ADG=90°,
∴△ABM≌△ADG,
∴∠GAD=∠BAM,AG=AM,
由(1)可得得:AP=PF,又∵AP⊥PF,
∴△APF是等腰直角三角形,
∴∠PAG=45°,
∵∠BAD=90°,
∴∠GAD+∠BAP=45°,
∴∠BAM+∠BAP=45°,
∴∠MAP=∠PAG=45°,
又∵AP=AP,
∴△PAM≌△PAG,
∴PM=PG,
∴△PCG的周长=PG+PC+CG,
=PM+PC+CG,
=PB+BM+PC+CG,
=PB+DG+PC+CG,
=BC+DC,
=2a;
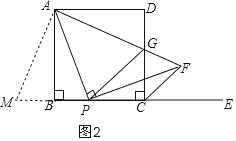
应用:如图3,∵PG∥CF,
∴∠PGC=∠GCF=45°,
∴△PCG是等腰直角三角形,
∴PC=CG,
设PB=x,则PC=CG=a﹣x,
由探究得:△PCG的周长=2a,
则PG+PC+CG=2a,
![]() PC+2PC=2a,
PC+2PC=2a,
![]() (a﹣x)=2a,
(a﹣x)=2a,
把![]() 代入得:
代入得: 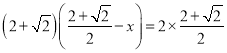
解得: ![]() ,即PB=
,即PB=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:一般地,
 个相同的因数
个相同的因数 相乘
相乘  ,记为
,记为 .如
.如 ,此时,
,此时, 叫做以
叫做以 为底
为底 的对数,记为
的对数,记为 (即
(即 ).一般地,若
).一般地,若 ,(
,( 且
且 ,
, ),则
),则 叫做以
叫做以 为底
为底 的对数,记为
的对数,记为 (即
(即 ).如
).如 ,则
,则 叫做以
叫做以 为底
为底 的对数,记为
的对数,记为 (即
(即 ).
).(1)计算以下各对数的值:
 __________,
__________, __________,
__________, __________.
__________.(2)观察(1)中三数
 、
、 ,
, 之间满足怎样的关系式,
之间满足怎样的关系式, 、
、 、
、 之间又满足怎样的关系式;
之间又满足怎样的关系式;(3)由(2)的结果,你能归纳出一个一般性的结论吗?
 __________.(
__________.( 且
且 ,
, ,
, )
)(4)根据幂的运算法则:
 以及对数的含义证明上述结论.
以及对数的含义证明上述结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
-
科目: 来源: 题型:
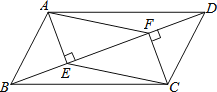
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AE⊥BD于E,CF⊥BD于F,连结AF,CE.求证:四边形AECF是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,求
,求 的最大值与最小值.
的最大值与最小值. -
科目: 来源: 题型:
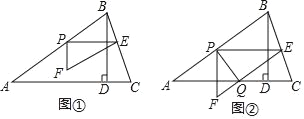
查看答案和解析>>【题目】如图①,在锐角△ABC中,AB=5,tanC=3,BD⊥AC于点D,BD=3,点P从点A出发,以每秒1个单位长度的速度沿AB向终点B运动,过点P作PE∥AC交边BC于点E,以PE为边作Rt△PEF,使∠EPF=90°,点F在点P的下方,且EF∥AB.设△PEF与△ABD重叠部分图形的面积为S(平方单位)(S>0),点P的运动时间为t(秒)(t>0).
(1)求线段AC的长.
(2)当△PEF与△ABD重叠部分图形为四边形时,求S与t之间的函数关系式.
(3)若边EF与边AC交于点Q,连结PQ,如图②.
①当PQ将△PEF的面积分成1:2两部分时,求AP的长.
②直接写出PQ的垂直平分线经过△ABC的顶点时t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P是正方形ABCD边AB上一点(不与A、B重合),连接PD并将线段PD绕点P顺时针旋转90°,得线段PE,连接BE,则∠CBE等于( )

A. 75°B. 60°C. 30°D. 45°
相关试题

