【题目】如图,BC为半圆的直径,O为圆心,D是弧AC的中点,四边形ABCD的对角线AC,BD交于点E,BC= ![]() ,CD=
,CD= ![]() ,则sin∠AEB的值为 .
,则sin∠AEB的值为 . 
参考答案:
【答案】![]()
【解析】解:∵BC为半圆的直径,
∴∠BAE=∠BDC=90°.
∵D是弧AC的中点,
∴∠ABE=∠DBC.
∴△ABE∽△DBC.
在Rt△DCB中,
∵∠BDC=90°,BC= ![]() ,CD=
,CD= ![]() ,
,
∴BD= ![]() ,
,
∴sin∠DCB=BD:BC= ![]() ,
,
∵△ABE∽△DBC,
∴∠AEB=∠DCB.
∴sin∠AEB= ![]() .
.
故答案为: ![]() .
.
根据直径所对的圆周角是直角得出∠BAE=∠BDC=90°.根据等弧所对的圆周角相等得出∠ABE=∠DBC ,从而判断出△ABE∽△DBC,在Rt△DCB中,根据勾股定理算出BD,从而根据正弦函数的定义得出sin∠DCB的值,根据相似三角形对应边成比例,及等角的同名三角函数值相等得出答案。
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数的自变量x满足
 ≤x≤2时,函数值y满足
≤x≤2时,函数值y满足  ≤y≤1,则下列函数①y=
≤y≤1,则下列函数①y=  x,②y=
x,②y=  ,③y=
,③y=  ,④y=﹣
,④y=﹣  x+
x+  ,⑤y=(x﹣1)2 , 符合条件的函数有( )
,⑤y=(x﹣1)2 , 符合条件的函数有( )
A.2个
B.3个
C.4个
D.5个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为等腰直角三角形,∠BAC=90°,BC=2,E为AB上任意一动点,以CE为斜边作等腰Rt△CDE,连接AD,下列说法:①∠BCE=∠ACD;②AC⊥ED;③△AED∽△ECB;④AD∥BC;⑤四边形ABCD的面积有最大值,且最大值为
 .其中,正确的结论是( )
.其中,正确的结论是( ) 
A.①②④
B.①③⑤
C.②③④
D.①④⑤ -
科目: 来源: 题型:
查看答案和解析>>【题目】 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫作格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
(1)在正方形网格中,画出△AB'C′;
(2)画出△AB′C′向左平移4格后的△A′B″C″;
(3)计算线段AB在变换到AB′的过程中扫过区域的面积.
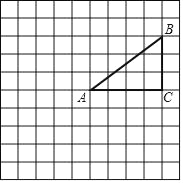
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB,CD是⊙O的两条互相垂直的直径,点O1 , O2 , O3 , O4分别是OA、OB、OC、OD的中点,若⊙O的半径为2,则阴影部分的面积为( )

A.8
B.4
C.4π+4
D.4π﹣4 -
科目: 来源: 题型:
查看答案和解析>>【题目】小丽手中有块长方形的硬纸片,其中长比宽多10cm,长方形的周长是100cm.
(1)求长方形的面积.
(2)现小丽想用这块长方形的硬纸片,沿着边的方向裁出一块长与宽的比为5:4,面积为520cm2的新纸片作为他用.试判断小丽能否成功,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(﹣1,﹣1),B(3,2),C(1,4)
(1)画出△ABC向上平移2个单位,向左平移3个位置后的△A′B′C′;
(2)写出A、C的对应点A′、C′的坐标;
(3)求两次平移过程中线段AC扫过的面积.

相关试题

