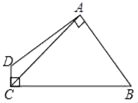
【题目】如图,在△OAB中,OA=OB,以点O为圆心的⊙O经过AB的中点C,直线AO与⊙O相交于点E、D,OB交⊙O于点F,P是 ![]() 的中点,连接CE、CF、BP.
的中点,连接CE、CF、BP. 
(1)求证:AB是⊙O的切线.
(2)若OA=4,则 ①当 ![]() 长为时,四边形OECF是菱形;
长为时,四边形OECF是菱形;
②当 ![]() 长为时,四边形OCBP是正方形.
长为时,四边形OCBP是正方形.
参考答案:
【答案】
(1)解:∵在△ABO中,OA=OB,C是AB的中点,
∴OC⊥AB.
∵OC为⊙O的半径,
∴AB是⊙O的切线.
(2)![]() ;
;![]()
【解析】(2)①∵OECF为菱形, ∴OE=EC,∠EOC=∠COF.
∴OE=EC=OC.
∴∠EOC=∠COF=60°.
∴∠DOF=60°.
又∵P为弧DF的中点,
∴∠DOP=30°.
∵∠AOC=60°,∠OCA=90°,
∴OC= ![]() OA=2.
OA=2.
∴弧DP的长= ![]() =
= ![]() .
.
②∵四边形OCBP为正方形,
∴∠COB=∠POB=45°.
∴OC= ![]() OB=2
OB=2 ![]() .
.
∵P为弧DF的中点,
∴∠DOP=45°.
∴弧DP的长= ![]() =
= ![]() .
.
所以答案是:① ![]() ;②
;② ![]() .
.
(1)由等腰三角形三线合一的性质可知OC⊥AB,依据题意可知OC为⊙O的半径,故此可证明AB是⊙O的切线;(2)①由菱形的性质可知:OE=EC,∠EOC=∠COF,然后证明△OEC为等边三角形可得到∠EOC的度数,然后可求得∠DOP的度数,接下来,在△OAC中,利用特殊锐角三角函数值可求得OC的长,最后依据弧长公式求解即可;②依据正方形的性质可求得OC= ![]() ,∠POF=45°,然后可得到∠DOP的度数,最后依据弧长公式求解即可.
,∠POF=45°,然后可得到∠DOP的度数,最后依据弧长公式求解即可.
【考点精析】本题主要考查了等腰三角形的性质和正方形的判定方法的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);先判定一个四边形是矩形,再判定出有一组邻边相等;先判定一个四边形是菱形,再判定出有一个角是直角才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(
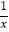 ﹣
﹣ 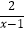 )÷
)÷  ,其中x的值从不等式组
,其中x的值从不等式组 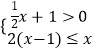 的整数解中选取.
的整数解中选取. -
科目: 来源: 题型:
查看答案和解析>>【题目】为创建国家文明城市,我市特在每个红绿灯处设置了文明监督岗,文明劝导员老牛某工作日在市中心的一个十字路口,对闯红灯的人数进行统计.根据上午7:00~12:00中各时间段闯红灯的人数制作了如图所示的尚不完整的统计图,请根据统计图解答下列问题:
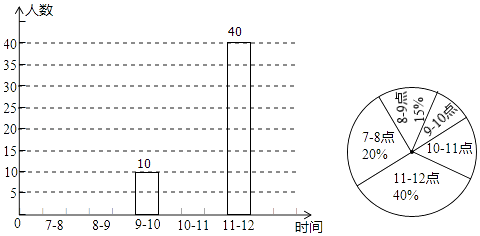
(1)该工作日7:00~12:00共有人闯红灯?
(2)①补全条形统计图, ②计算扇形统计图中10~11点所对应的圆心角的度数.
(3)该工作日7:00~12:00,各时间段闯红灯的人数的方差是
(4)请你根据统计图提供的信息向交通管理部门提出一条合理化建议. -
科目: 来源: 题型:
查看答案和解析>>【题目】若实数m、n满足等式
 ,且m、n恰好是等腰△ABC的两条边的边长,则△ABC的周长是_______.
,且m、n恰好是等腰△ABC的两条边的边长,则△ABC的周长是_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某河大堤上有一颗大树ED,小明在A处测得树顶E的仰角为45°,然后沿坡度为1:2的斜坡AC攀行20米,在坡顶C处又测得树顶E的仰角为76°,已知ED⊥CD,并且CD与水平地面AB平行,求大树ED的高度.(精确到1米)
(参考数据:sin76°≈0.97,cos76°=0.24,tan76°≈4.01, =2.236)
=2.236)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AB∥DE,AC∥DF,AC=DF下列条件中,不能判断△ABC≌△DEF的是( )

A. AB=DE B. ∠B=∠E C. EF=BC D. EF∥BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为_____.
相关试题

